题目内容
设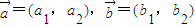
，定义一种向量积
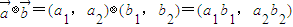．已知
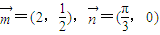，点P（x，y）在y=sinx的图象上运动，点Q在y=f（x）的图象上运动，且满足
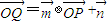（其中O为坐标原点），则y=f（x）的最大值为 ．
【答案】分析：设Q（x，y），P（x′，y′）根据题目中给出的定义方式，得出两点坐标的关系，进一步求出函数y=f（x）的解析式，再求最大值．
解答：解：设Q（x，y），P（x′，y′）则由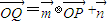
得（x，y）=（2x′，
sinx′）+
∴
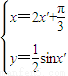消去x′得y=f（x）的解析式为
，x∈R
易得y=f（x）的最大值为
．
故答案为：
．
点评：本题是新定义式的题目，理解、使用新定义将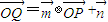
化简得出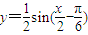
是关键．考查阅读理解、分析解决、转化的能力．
解答：解：设Q（x，y），P（x′，y′）则由
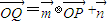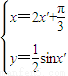得（x，y）=（2x′，sinx′）+∴ 消去x′得y=f（x）的解析式为，x∈R易得y=f（x）的最大值为
．故答案为：
．点评：本题是新定义式的题目，理解、使用新定义将
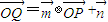化简得出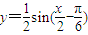 是关键．考查阅读理解、分析解决、转化的能力． 
练习册系列答案
相关题目
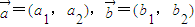，定义一种向量积
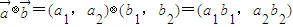．已知
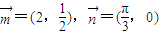，点P（x，y）在y=sinx的图象上运动，点Q在y=f（x）的图象上运动，且满足
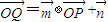（其中O为坐标原点），则y=f（x）的最大值为 ．
，定义一种向量积：
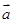
＝(a1b1，a2b2)．已知点
，
＝，
＝，点Q在y＝f(x)的图象上运动，满足
＝
＋
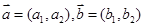，定义一种向量积：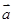
＝
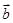(a1b1，a2b2)．已知点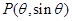
，
＝， 
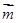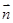＝，点Q在y＝f(x)的图象上运动，满足
＝
＋
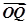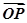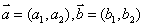，定义一种向量积：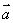
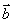＝（a1b1，a2b2）．已知点
，
＝，
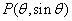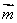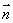＝，点Q在y＝f（x）的图象上运动，满足
＝
＋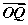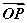