题目内容
如图所示,在长方体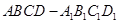 中,
中,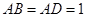 ,
,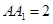 ,
,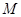 是棱
是棱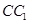 上一点,
上一点,
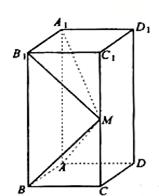
(1)若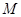 为CC1的中点,求异面直线A1M和C1D1所成的角的正切值;
为CC1的中点,求异面直线A1M和C1D1所成的角的正切值;
(2)是否存在这样的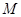 ,使得平面ABM⊥平面A1B1M,若存在,求出
,使得平面ABM⊥平面A1B1M,若存在,求出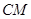 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
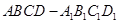 中,
中,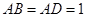 ,
,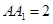 ,
,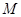 是棱
是棱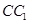 上一点,
上一点,
(1)若
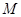 为CC1的中点,求异面直线A1M和C1D1所成的角的正切值;
为CC1的中点,求异面直线A1M和C1D1所成的角的正切值;(2)是否存在这样的
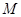 ,使得平面ABM⊥平面A1B1M,若存在,求出
,使得平面ABM⊥平面A1B1M,若存在,求出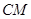 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。(1)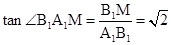 。(2)
。(2)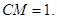
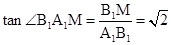 。(2)
。(2)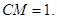
试题分析:(1)由于C1D1∥B1A1故根据异面直线所成角的定义可知∠MA1B1为异面直线A1M和C1D1所成的角然后在解三角形MA1B1求出∠MA1B1的正切值即可.
(Ⅱ)可根据题中条件设出点M的坐标,然后根据面面垂直,计算得出A1B1⊥BM,BM⊥B1M然后再根据面面垂直的判定定理即可得证.
解:(1)∵C1D1∥A1B1
∴∠B1A1M即为直线A1M和C1D1所成的角
∴
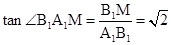 。
。(2)建立坐标系:
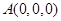 ,
,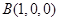 ,
,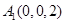 ,
,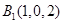 ,
,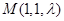
在平面
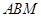 上选择向量
上选择向量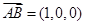 ,
,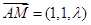 ,设法向量
,设法向量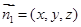
由
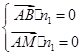 ,解得
,解得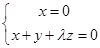 ,取
,取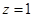 ,得
,得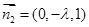
在平面
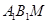 上选择向量
上选择向量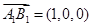 ,
,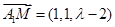 ,设法向量
,设法向量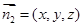
由
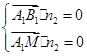 ,解得
,解得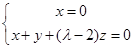 ,取
,取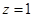 ,得
,得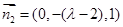 ,
,由
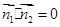 ,
,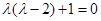 ,解得
,解得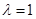 ,所以
,所以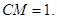
点评:解题的关键是要掌握异面直线所成角的定义(即将异面直线转化为相交直线所成的角)和面面垂直的判定定理。

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 平面上的射影,则等于( )
平面上的射影,则等于( )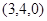
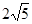
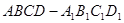 的棱长为2,则异面直线
的棱长为2,则异面直线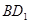 与AC之间的距离为_________。
与AC之间的距离为_________。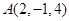 、
、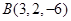 、
、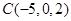 ,则
,则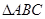 的中线
的中线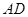 的长为( ).
的长为( ).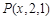 到
到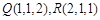 的距离相等,则
的距离相等,则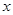 的值为( ).
的值为( ). 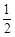
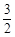
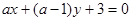 的距离
的距离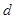 为最大时,
为最大时,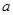 的值依次为 ( )
的值依次为 ( )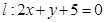 上的点与原点的距离的最小值是
上的点与原点的距离的最小值是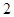
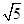
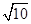
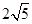
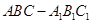 的各棱长都为1,
的各棱长都为1,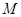 为
为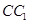 的中点,则点
的中点,则点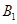 到截面
到截面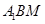 的距离为
的距离为