题目内容
设函数f(x)(x∈R)为奇函数,f(1)= ,
, f(x+2)=f(x)+f(2),则f(5)=
f(x+2)=f(x)+f(2),则f(5)=
| A.0 | B.1 | C.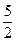 | D.5 |
C
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知偶函数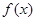 在区间
在区间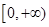 单调递增,
单调递增,
则满足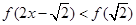 的
的 取值
取值
范围是( )
A.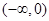 | B.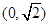 |
C.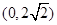 | D.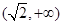 |
已知函数f(x)=若f(a)=,则a=
( )
| A.-1 | B. |
| C.-1或 | D.1或- |
设偶函数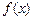 对任意
对任意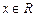 ,都有
,都有 ,且当
,且当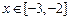 时,
时,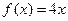 ,
,
则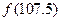 =" "
=" "
| A.10 | B. | C.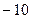 | D.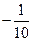 |
已知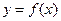 是偶函数,当
是偶函数,当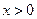 时,
时, ,当
,当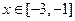 时,
时, 恒成立,则
恒成立,则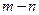 的最小值是
的最小值是
A.  | B.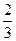 | C. | D.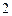 |
.已知奇函数f(x)满足f(-1)=f(3)=0,在区间[-2,0)上是减函数,在区间[2,+∞)是增函数,函数F(x)=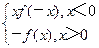 ,则{x|F(x)>0}=
,则{x|F(x)>0}=
| A.{x|x<-3,或0<x<2,或x>3} |
| B.{x|x<-3,或-1<x<0,或0<x<1,或x>3} |
| C.{x|-3<x<-1,或1<x<3} |
| D.{x|x<-3,或0<x<1,或1<x<2,或2<x<3} |
 与指数函数
与指数函数 的图像只可能是
的图像只可能是
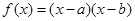 (其中
(其中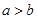 )的图象如下面右图所示,则函数
)的图象如下面右图所示,则函数 的图象是
的图象是
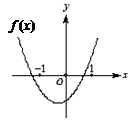
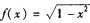 在区间/)上的反函数是它本身,则D可以是
在区间/)上的反函数是它本身,则D可以是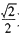 ) D
) D .〔
.〔 ,1〕
,1〕