题目内容
设等差数列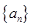 的公差
的公差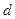 ≠0,
≠0,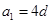 .若
.若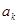 是
是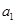 与
与 的等比中项,则
的等比中项,则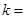 ( )
( )
| A.3或 -1 | B.3或1 | C.3 | D.1 |
C
解析试题分析:因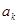 是
是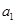 与
与 的等比中项,所以
的等比中项,所以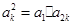 ,即
,即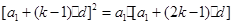 ,又
,又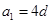 ,
,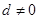 ,则有
,则有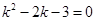 ,即
,即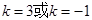 (舍去).
(舍去).
考点:等差数列的通项公式及等差数列的性质.

练习册系列答案
相关题目
已知等比数列 中,各项都是正数,且
中,各项都是正数,且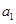 ,
,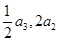 成等差数列,则
成等差数列,则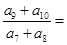 ( )
( )
A.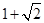 | B.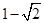 | C.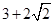 | D.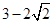 |
各项都是正数的等比数列 的公比
的公比 ,且
,且 成等差数列,则
成等差数列,则 的值为( )
的值为( )
A.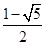 | B.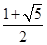 |
C. | D.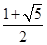 或 或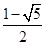 |
在等差数列 中,
中, ,则此数列前13项的和为 ( )
,则此数列前13项的和为 ( )
A.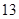 | B. | C.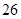 | D.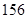 |
已知等比数列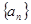 的首项
的首项 公比
公比 ,则
,则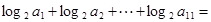 ( )
( )
| A.50 | B.35 | C.55 | D.46 |
等差数列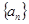 中的
中的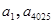 是函数
是函数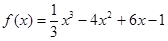 的极值点,则
的极值点,则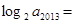 ( )
( )
A.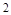 | B.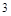 | C. | D.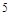 |
设等差数列 的前
的前 项和为
项和为 ,且
,且 ,
, ,则
,则 ( )
( )
| A.60 | B.70 | C.90 | D.40 |
某辆汽车购买时的费用是15万元,每年使用的保险费、路桥费、汽油费等约为1.5万元.年维
修保养费用第一年3000元,以后逐年递增3000元,则这辆汽车报废的最佳年限(即使用多少年的年平均费用最少)是 ( )
| A.8年 | B.10年 | C.12年 | D.15年 |
等差数列{an}中,已知a1=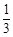 ,a2+a5=4,an=33,则n的值为( ).
,a2+a5=4,an=33,则n的值为( ).
| A.50 | B.49 | C.48 | D.47 |