题目内容
已知变量x，y满足关系式
，z=x2+（y+1）2，则z的最大值是
|
25
25
．分析：作出不等式组表示的平面区域，由于z=x2+（y+1）2的几何意义是平面区域内的点P（x，y）与定点M（0，-1）的距离的平方，结合图形可求Z的最大值
解答：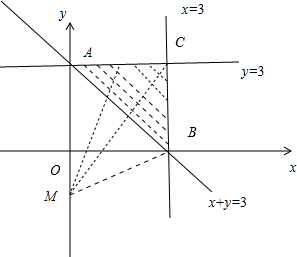
解：作出不等式组表示的平面区域，如图所示的阴影部分
由于z=x2+（y+1）2的几何意义是平面区域内的点P（x，y）与定点M（0，-1）的距离的平方
结合图形可知，MC为距离的最大值，由
可得C（3，3）
此时Z=（3-0）2+（3+1）2=25
故答案为25
解：作出不等式组表示的平面区域，如图所示的阴影部分由于z=x2+（y+1）2的几何意义是平面区域内的点P（x，y）与定点M（0，-1）的距离的平方
结合图形可知，MC为距离的最大值，由
|
此时Z=（3-0）2+（3+1）2=25
故答案为25
点评：本题主要考查了线性规划在距离求解中的应用，解答本题的关键是准确理解z=x2+（y+1）2的几何意义．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
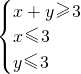，z=x2+（y+1）2，则z的最大值是________．
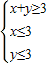，z=x2+（y+1）2，则z的最大值是 ．
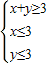，z=x2+（y+1）2，则z的最大值是 ．
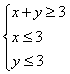，z=x2+（y+1）2，则z的最大值是（ ）。