题目内容
(本小题8分)
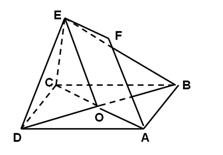
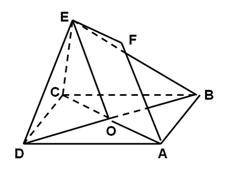
如图,正方形ABCD和四边形ACEF所在的平面互相垂直. EF//AC,AB= ,CE=EF=1,
,CE=EF=1, .
.
(1)求证:AF//平面BDE;
(2)求异面直线AB与DE所成角的余弦值.
【答案】
(1)略
(2)
【解析】(1)证明: 是正方形,且AB=
是正方形,且AB=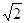 ,
,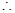 AO=1,又
AO=1,又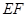 //
//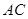 ,EF=1,
,EF=1,
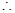 EFAO为平行四边形,则
EFAO为平行四边形,则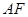 //
//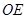 ,而
,而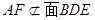 ,
,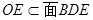 ,
,
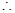 AF//面BDE ………………………………………………(3分)
AF//面BDE ………………………………………………(3分)
(2)解: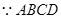 是正方形,
是正方形,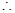
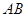 //
//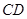
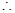
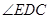 为异面直线AB与DE所成的角或其补角
…………………………(2分)
为异面直线AB与DE所成的角或其补角
…………………………(2分)
又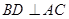 ,又面ABCD
,又面ABCD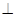 面ACEF,且面ABCD
面ACEF,且面ABCD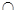 面ACEF=AC
面ACEF=AC
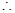 BD
BD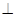 面ACEF,又
面ACEF,又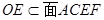 ,
,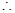 BD
BD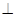 OE.
OE.
而由EC=1,OC=OA=1,
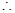 OE=1,又OD=1,则ED=
OE=1,又OD=1,则ED=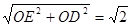
又CD=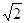 ,CE=1,
,CE=1,
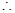
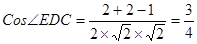
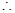 异面直线AB与DE所成的角的余弦值为
异面直线AB与DE所成的角的余弦值为 ……………………………………(3分)
……………………………………(3分)

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目

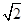 ,CE=EF=1,
,CE=EF=1,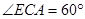 .
.
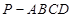 中,
中, 平面
平面 ,
, ,
, ,
,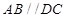 ,
,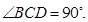
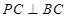 ;
;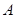 到平面
到平面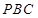 的距离
的距离 平面
平面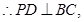 又
又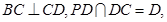
 平面
平面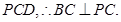 (4分)
(4分)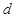 ,
, ,
, ,
, 即点
即点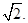 (8分)
(8分) 中,底面
中,底面 是矩形,
是矩形,
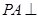 平面
平面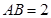 ,
, ,以
,以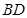 的中点
的中点 为球心、
为球心、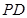 于点
于点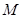 .
.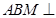 平面
平面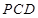 ;
; 的距离.
的距离. 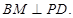
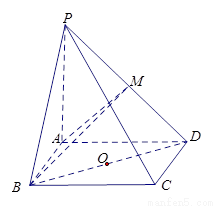
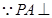 平面
平面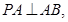
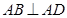 ,
,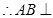 平面
平面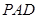 ,
,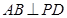 ,
,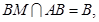
 平面
平面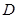 到平面
到平面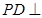 平面
平面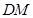 的长就是点
的长就是点
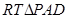 中,
中,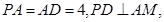
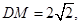 (7分)
(7分)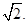 (8分)
(8分)