题目内容
甲、乙两位同学玩游戏,对于给定的实数a1,按下列方法操作一次产生一个新的实数:由甲、乙同时各抛一枚均匀的硬币,如果出现两个正面朝上或两个反面朝上,则把a1乘以2后再减去12;如果出现一个正面朝上,一个反面朝上,则把a1除以2后再加上12,这样就可得到一个新的实数a2,对a2仍按上述方法进行一次操作,又得到一个新的实数a3,当a3>a1时,甲获胜,否则乙获胜.若甲获胜的概率为
,则a1的取值范围是
| 3 | 4 |
(-∞,12]∪[24,+∞)
(-∞,12]∪[24,+∞)
.分析:按要求操作一次产生一个新的实数,实际上这是一个新定义问题,列举得到新的实数的途径,列出不等式,根据所给的甲获胜的概率为
,可求a1的取值范围.
| 3 |
| 4 |
解答:解:由题意得,a3的结果有四种:
1.a1→2a1-12→2(2a1-12)-12=4a1-36=a3,
2.a1→2a1-12→
(2a1-12)+12=a1+6=a3,
3.a1→
a1+12→
(
a1+12)+12=
a1+18=a3,
4.a1→
a1+12→2(
a1+12)-12=a1+18=a3,
每一个结果出现的概率都是
∵a1+18>a1,a1+6>a1,
∴要使甲获胜的概率为
,即a3>a1的概率为
,
∴4a1-36>a1,
a1+18≤a1,
或4a1-36≤a1,
a1+18>a1,
解得a1≥24或a1≤12.
故a1的取值范围是(-∞,12]∪[24,+∞)
故答案为:(-∞,12]∪[24,+∞)
1.a1→2a1-12→2(2a1-12)-12=4a1-36=a3,
2.a1→2a1-12→
| 1 |
| 2 |
3.a1→
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
4.a1→
| 1 |
| 2 |
| 1 |
| 2 |
每一个结果出现的概率都是
| 1 |
| 4 |
∵a1+18>a1,a1+6>a1,
∴要使甲获胜的概率为
| 3 |
| 4 |
| 3 |
| 4 |
∴4a1-36>a1,
| 1 |
| 4 |
或4a1-36≤a1,
| 1 |
| 4 |
解得a1≥24或a1≤12.
故a1的取值范围是(-∞,12]∪[24,+∞)
故答案为:(-∞,12]∪[24,+∞)
点评:本题考查新定义,考查生分析问题、解决问题,理解题意有些麻烦,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
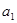 ,按下列方法操作一次产生一个新的实数:由甲、乙同时各抛一枚均匀的硬币,如果出现两个正面朝上或两个反面朝上,则把
,按下列方法操作一次产生一个新的实数:由甲、乙同时各抛一枚均匀的硬币,如果出现两个正面朝上或两个反面朝上,则把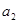 ,对
,对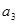 ,当
,当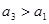 时,甲获胜,否则乙获胜。若甲获胜的概率为
时,甲获胜,否则乙获胜。若甲获胜的概率为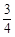 ,则
,则 ,则a1的取值范围是( )
,则a1的取值范围是( )