题目内容
已知⊿ABC中，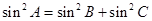
且，2cosB·sinC=sinA，则此三角形是（ ）
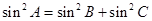且，2cosB·sinC=sinA，则此三角形是（ ）| A．直角三角形 | B．等腰三角形 | C．等腰直角三角形 | D．等边三角形 |
C
根据正弦定理，由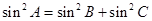可得
，
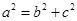所以该三角形是直角三角形。
因为2cosB·sinC=sinA，
所以2cosB·sinC=sin(B+C),
所以2cosB·sinC=sinB·cosC+cosB·sinC,
所以sinB·cosC-cosB·sinC=0
所以sin(B-C)=0,
所以B=C，
所以该三角形是等腰直角三角形。
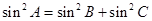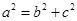可得，所以该三角形是直角三角形。
因为2cosB·sinC=sinA，
所以2cosB·sinC=sin(B+C),
所以2cosB·sinC=sinB·cosC+cosB·sinC,
所以sinB·cosC-cosB·sinC=0
所以sin(B-C)=0,
所以B=C，
所以该三角形是等腰直角三角形。
练习册系列答案
一线名师提优试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
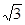，第三边上的中线长为2，则三角形的外接圆半径为 
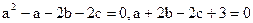，求这个三角形的最大内角.
中，
，则
的取值范围是 
，B，C，设△ABC三边长分别为a，b，c，则[
＋
＋
＝________
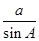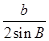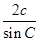中，
，
，
，则
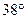方向，距小岛3海里的B处，发现隐藏在小岛边上的一艘走私船正开始向岛北偏西
方向行驶，测得其速度为10海里/小时，问巡逻艇需用多大的速度朝什么方向行驶，恰好用0.5小时在C处截住该走私船？
）
,
,
, 
,则
______ _____