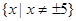题目内容
(本题满分12分)已知函数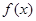 =
=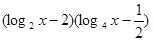 ,2≤
,2≤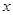 ≤4
≤4
(1)求该函数的值域;
(2)若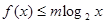 对于
对于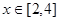 恒成立,求
恒成立,求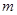 的取值范围.
的取值范围.
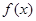 =
=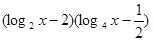 ,2≤
,2≤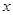 ≤4
≤4(1)求该函数的值域;
(2)若
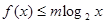 对于
对于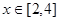 恒成立,求
恒成立,求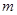 的取值范围.
的取值范围. (1)函数的值域是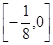 ;(2)
;(2)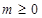
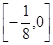 ;(2)
;(2)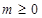
试题分析:(1)运用整体的思想,令对数式为t,得到t的二次函数的性质来得到求解。
(2)要证明不等式恒成立,只要证明函数的最值求解不等式。
解:(1)y =(
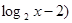 (
(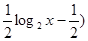 =
=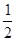
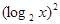 -
-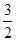
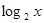
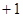
令
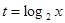 ,则
,则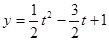
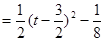
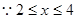
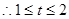
当
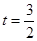 时,
时,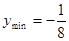 ,当
,当 或2时,
或2时,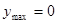
 函数的值域是
函数的值域是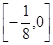
(2)令
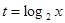 ,可得
,可得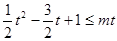 对于
对于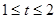 恒成立。
恒成立。所以
 对于
对于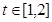 恒成立
恒成立设
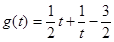 ,
,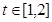
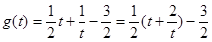
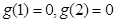 所以
所以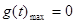 ,所以
,所以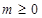 考点:
考点:点评:解决该试题的关键是将对数式作为整体来分析,构造二次函数的思想,进而转化为常规函数来求解不等式,以及函数的最值问题。

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
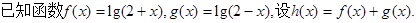

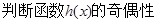 ,并说明理由.
,并说明理由.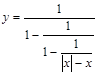
 时,函数
时,函数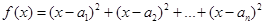 取得最小值。
取得最小值。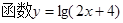 的定义域是
的定义域是 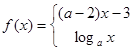
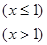 在R上单调递增,则实数
在R上单调递增,则实数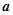 的取值范围为________
的取值范围为________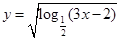 的定义域是( ).
的定义域是( ).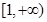

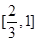
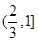
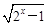 (a>0,a≠1).
(a>0,a≠1).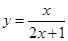 的值域为 .
的值域为 .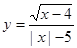 的定义域为( )z
的定义域为( )z