题目内容
（12分）设函数
.
(1)判断函数
奇偶性；
（2）证明：
的导数
；
(3) 求函数在区间
的最大值和最小值(结果用分式表示).
解析:（1）∵
,
,
∴函数
的定义域为实数R. ……1分
又∵
∴函数为奇函数. ……4分
（2）
的导数
． ……6分
由于
，故
．
（当且仅当
时，等号成立）． ……8分
(3)由（2）可知函数在
单调递增，所以在区间
上也单调递增，
故函数在
处取得最大值，最大值为
……10分
在
处取得最大值，最大值为
……12分
.ks5u.com
练习册系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
其中
上的单调性．
．
. （1） 判断
在区间
上的增减性并证明之；（2） 若不等式
≤
≤
对
恒成立, 求实数
≤
，若
，求证：
≥
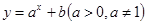的图象过
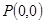与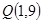
两点,设函数
;
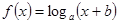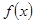的定义域;
的值域，判断g(x)奇偶性,并说明理由.
．
的奇偶性；
上增减性，并进行证明；
时，不等式
恒成立，求实数
的取值范围．
．
的奇偶性；
上增减性，并进行证明；
时，不等式
恒成立，求实数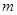
的取值范围．