题目内容
已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]()
![]() ,
,![]() ,设
,设![]() ,若
,若![]() 对一切
对一切![]() 恒成立,求
恒成立,求![]() 范围
范围
![]()
解析:
![]()
得![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,所以
,所以![]()
![]() ,所以
,所以![]()
![]() ,设
,设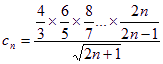
则
即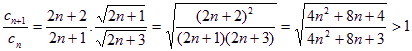
所以![]() 单调递增,当
单调递增,当![]() 时,
时,![]() 最小值为
最小值为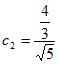
![]()
由![]() 得
得![]()
![]() 恒成立,故
恒成立,故![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]()
![]() ,
,![]() ,设
,设![]() ,若
,若![]() 对一切
对一切![]() 恒成立,求
恒成立,求![]() 范围
范围
![]()
![]()
得![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,所以
,所以![]()
![]() ,所以
,所以![]()
![]() ,设
,设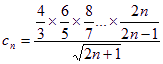
则
即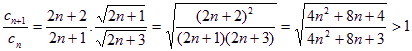
所以![]() 单调递增,当
单调递增,当![]() 时,
时,![]() 最小值为
最小值为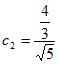
![]()
由![]() 得
得![]()
![]() 恒成立,故
恒成立,故![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案