题目内容
已知直线l过椭圆E:x2+2y2=2的右焦点F,且与E相交于P,Q两点.
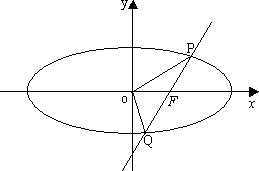
①设![]() (O为原点),求点R的轨迹方程;
(O为原点),求点R的轨迹方程;
②若直线l的倾斜角为60°,求![]() 的值.
的值.
答案:
解析:
解析:
解:①设![]()
![]()
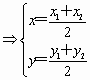 1分
1分
由![]() ,易得右焦点
,易得右焦点![]() 2分
2分
当直线l⊥x轴时,直线l的方程是:![]() ,根据对称性可知
,根据对称性可知![]() 3分
3分
当直线![]() 的斜率存在时,可设直线l的方程为
的斜率存在时,可设直线l的方程为![]()
代入E有![]()
![]() ;
;![]() 5分
5分
于是![]()
![]()
![]() ;
;![]()
消去参数![]() 得
得![]()
而![]() 也适上式,故R的轨迹方程是
也适上式,故R的轨迹方程是![]() 8分
8分
②设椭圆另一个焦点为![]() ,
,
在![]() 中
中![]() 设
设![]() ,则
,则![]()
由余弦定理得![]()
![]() 9分
9分
同理,在![]() ,设
,设![]() ,则
,则![]()
也由余弦定理得![]()
![]() 11分
11分
于是![]() 12分
12分
注:其它方法相应给分.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 已知直线l过椭圆E:x2+2y2=2的右焦点F,且与E相交于P,Q两点.
已知直线l过椭圆E:x2+2y2=2的右焦点F,且与E相交于P,Q两点. 已知直线l过椭圆E:x2+2y2=2的右焦点F,且与E相交于P,Q两点.
已知直线l过椭圆E:x2+2y2=2的右焦点F,且与E相交于P,Q两点.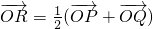 (O为原点),求点R的轨迹方程;
(O为原点),求点R的轨迹方程;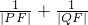 的值.
的值.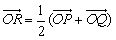 (O为原点),求点R的轨迹方程;
(O为原点),求点R的轨迹方程;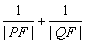 的值。
的值。 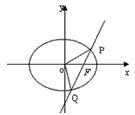
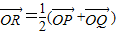 (O为原点),求点R的轨迹方程;
(O为原点),求点R的轨迹方程;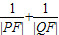 的值.
的值.