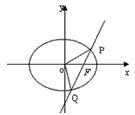
题目内容
已知直线l过椭圆E:x2+2y2=2的右焦点F,且与E相交于P,Q两点.(1)设
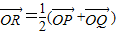 (O为原点),求点R的轨迹方程;
(O为原点),求点R的轨迹方程;(2)若直线l的倾斜角为60,求
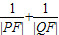 的值.
的值.
【答案】分析:(1)可设直线l的方程为y=k(x-1),将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用向量关系式即可求得R的轨迹方程;
(2)设椭圆另一个焦点为F',在△PF'F中由余弦定理m的值,同理,在△QF'F,设|QF|=n,也由余弦定理得n的值,最后即可求得 的值.
的值.
解答:解:(1)设P(x1,y1),Q(x2,y2),R(x,y)
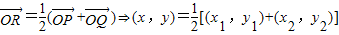
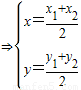
由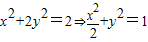 ,易得右焦点F(1,0)
,易得右焦点F(1,0)
当直线l⊥x轴时,直线l的方程是:x=1,根据对称性可知R(1,0)
当直线l的斜率存在时,可设直线l的方程为y=k(x-1)
代入E有(2k2+1)x2-4k2x+2k2-2=0△=8k2+8>0; (5分)
(5分)
于是R(x,y):x=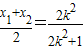 ; y=k(x-1)
; y=k(x-1)
消去参数k得x2+2y2-x=0而R(1,0)也适上式,故R的轨迹方程是x2+2y2-x=0
(2)设椭圆另一个焦点为F',
在△PF'F中∠PFF'=120,|F'F|=2,设|PF|=m,则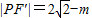
由余弦定理得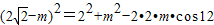
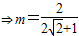
同理,在△QF'F,设|QF|=n,则
也由余弦定理得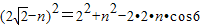

于是
点评:本题考查椭圆的长轴和短轴的长,焦点的坐标的求法、轨迹方程、直线与圆锥曲线的综合问题.解题时要认真审题,注意椭圆性质的合理运用.
(2)设椭圆另一个焦点为F',在△PF'F中由余弦定理m的值,同理,在△QF'F,设|QF|=n,也由余弦定理得n的值,最后即可求得
 的值.
的值.解答:解:(1)设P(x1,y1),Q(x2,y2),R(x,y)
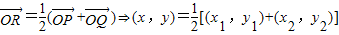
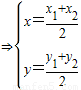
由
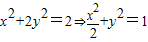 ,易得右焦点F(1,0)
,易得右焦点F(1,0)当直线l⊥x轴时,直线l的方程是:x=1,根据对称性可知R(1,0)
当直线l的斜率存在时,可设直线l的方程为y=k(x-1)
代入E有(2k2+1)x2-4k2x+2k2-2=0△=8k2+8>0;
 (5分)
(5分)于是R(x,y):x=
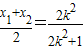 ; y=k(x-1)
; y=k(x-1)消去参数k得x2+2y2-x=0而R(1,0)也适上式,故R的轨迹方程是x2+2y2-x=0
(2)设椭圆另一个焦点为F',
在△PF'F中∠PFF'=120,|F'F|=2,设|PF|=m,则
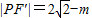
由余弦定理得
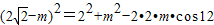
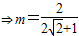
同理,在△QF'F,设|QF|=n,则

也由余弦定理得
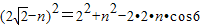

于是

点评:本题考查椭圆的长轴和短轴的长,焦点的坐标的求法、轨迹方程、直线与圆锥曲线的综合问题.解题时要认真审题,注意椭圆性质的合理运用.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
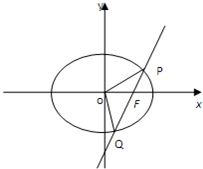 已知直线l过椭圆E:x2+2y2=2的右焦点F,且与E相交于P,Q两点.
已知直线l过椭圆E:x2+2y2=2的右焦点F,且与E相交于P,Q两点.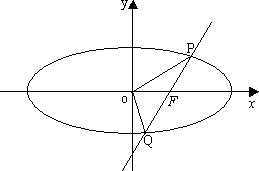
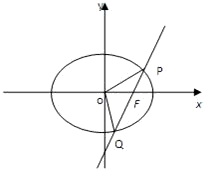 已知直线l过椭圆E:x2+2y2=2的右焦点F,且与E相交于P,Q两点.
已知直线l过椭圆E:x2+2y2=2的右焦点F,且与E相交于P,Q两点.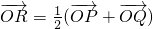 (O为原点),求点R的轨迹方程;
(O为原点),求点R的轨迹方程;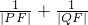 的值.
的值.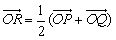 (O为原点),求点R的轨迹方程;
(O为原点),求点R的轨迹方程;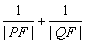 的值。
的值。