Question

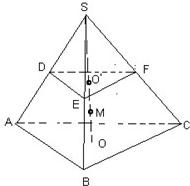
已知球O是棱长为12的正四面体S-ABC的外接球，D，E，F分别是棱SA，SB，SC的中点，则平面DEF截球O所得截面的面积是

 

．

Answer 1

分析：作出图形，设M点球心，O′为截面圆的圆心，求出MO′的距离，再求截面圆的半径，求出平面DEF截球O所得截面的面积．

解答：解：作图如图，设M点球心，可为高SO的四等分点处，
O′为截面圆的圆心，可知其在高的中点处，
易求出SO=4

6

，∴SM=

3

4

×4

6

=3

6

.
S0′=

1

2

×4

6

=2

6

∴EO′=

6

∴r=

(3 6 )2- 6 2

=4

3

∴s=πr²=48π．
故答案为：48π

点评：本题考查棱锥的结构特征，几何体的外接球的知识，考查计算能力，是基础题．