题目内容
在边长为1的正方形ABCD内随机取一点P,则点P到点A的距离大于1的概率为( )
A、
| ||
B、1-
| ||
C、
| ||
D、1-
|
分析:由题意作出如图的图形,四边形ABCD是边长为1的正方形,其中的圆弧是半径为1的圆面的
,故阴影部分的面积易求,概率易求
| 1 |
| 4 |
解答: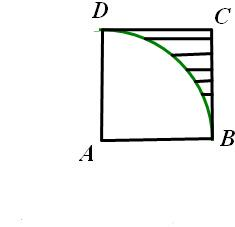 解:如图,四边形ABCD是边长为1的正方形,其中的圆弧是半径为1的圆面的
解:如图,四边形ABCD是边长为1的正方形,其中的圆弧是半径为1的圆面的
,
正方形的面积是1,
圆面的面积是
,
故阴影部分的面积是1-
,
则点P到点A的距离大于1的概率为
=1-
,
故选B.
 解:如图,四边形ABCD是边长为1的正方形,其中的圆弧是半径为1的圆面的
解:如图,四边形ABCD是边长为1的正方形,其中的圆弧是半径为1的圆面的| 1 |
| 4 |
正方形的面积是1,
| 1 |
| 4 |
| π |
| 4 |
故阴影部分的面积是1-
| π |
| 4 |
则点P到点A的距离大于1的概率为
1-
| ||
| 1 |
| π |
| 4 |
故选B.
点评:本题考查几何概率模型,解题的关键是掌握几何概率模型的定义及求解方法,选定研究对象,作出对应的图形,求出相应的测试,如本题求的是面积,然后利用几何概率模型的求概率公式求出事件发生的概率.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
在边长为1的正方形ABCD中任取一点P,则△ABP的面积大于
的概率是 ( )
| 1 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
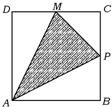
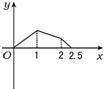
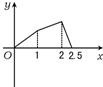
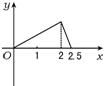
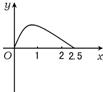
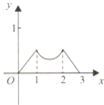
 如右图所示,点P在边长为1的正方形的边上运动,设M是CD边的中点,则当点P沿着A-B-C-M运动时,以点P经过的路程x为自变量,三角形APM的面积函数的图象形状大致是( )
如右图所示,点P在边长为1的正方形的边上运动,设M是CD边的中点,则当点P沿着A-B-C-M运动时,以点P经过的路程x为自变量,三角形APM的面积函数的图象形状大致是( )



 如图,动点P在边长为1的正方形ABCD的边上沿ABCD运动,x表示动点P由A点出发所经过的路程,y表示△APD的面积,则函数y=f(x)的图象的草图是( )
如图,动点P在边长为1的正方形ABCD的边上沿ABCD运动,x表示动点P由A点出发所经过的路程,y表示△APD的面积,则函数y=f(x)的图象的草图是( )