题目内容
已知点A、B、C的坐标分别为A(3,0)、B(0,3)、C(cosα,sinα).
(1)若|
|=|
|,α∈(
,
).求角α的值;
(2)若
•
=-1,求
的值.
(1)若|
| AC |
| BC |
| π |
| 2 |
| 3π |
| 2 |
(2)若
| AC |
| BC |
| sin2α+sinαcosα |
| 1+tanα |
分析:(1)由题意可得
,
的坐标,进而可得模长,可得sinα=cosα,结合α的范围可得答案;(2)由
•
=-1可得sinα+cosα=
.两边平方得
2sinαcosα=-
,而
=
=sinαcosα,代入可得.
| AC |
| BC |
| AC |
| BC |
| 2 |
| 3 |
2sinαcosα=-
| 5 |
| 9 |
| sin2α+sinαcosα |
| 1+tanα |
| sinα(sinα+cosα) | ||
1+
|
解答:解:(1)∵
=(cosα-3,sinα),
=(cosα,sinα-3),
∴|
|=
=
,
|
|=
=
.
由|
|=|
|得sinα=cosα.…(4分)
又∵α∈(
,
),∴α=
.…(6分)
(2)由
•
=-1可得(cosα-3)cosα+sinα(sinα-3)=-1.
∴sinα+cosα=
.两边平方得
1+2sinαcosα=
,∴2sinαcosα=-
.…(8分)
又
=
=sinαcosα.
∴
=-
…(12分)
| AC |
| BC |
∴|
| AC |
| (cosα-3)2+sin2α |
| 10-6cosα |
|
| BC |
| cos2α+(sinα-3)2 |
| 10-6sinα |
由|
| AC |
| BC |
又∵α∈(
| π |
| 2 |
| 3π |
| 2 |
| 5π |
| 4 |
(2)由
| AC |
| BC |
∴sinα+cosα=
| 2 |
| 3 |
1+2sinαcosα=
| 4 |
| 9 |
| 5 |
| 9 |
又
| sin2α+sinαcosα |
| 1+tanα |
| sinα(sinα+cosα) | ||
1+
|
∴
| sin2α+sinαcosα |
| 1+tanα |
| 5 |
| 18 |
点评:本题考查平面向量数量积的坐标表示,涉及三角函数的运算,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (a >0)与x轴的正半轴交于点P.点Q的坐
(a >0)与x轴的正半轴交于点P.点Q的坐 =6.
=6.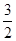 的直线交椭圆C于A、B两点,求△AOB的面积
的直线交椭圆C于A、B两点,求△AOB的面积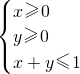 ,恒有(a+b,a-b)在不等式组对应的区域内,则以a,b为坐标的点P (a,b)所形成的平面区域的面积是
,恒有(a+b,a-b)在不等式组对应的区域内,则以a,b为坐标的点P (a,b)所形成的平面区域的面积是

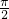

 ,下列所给出的不能表示此点的坐标的是
,下列所给出的不能表示此点的坐标的是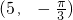
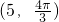
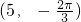
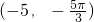
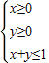 ,恒有(a+b,a-b)在不等式组对应的区域内,则以a,b为坐标的点P (a,b)所形成的平面区域的面积是( )
,恒有(a+b,a-b)在不等式组对应的区域内,则以a,b为坐标的点P (a,b)所形成的平面区域的面积是( )



 ,焦点是
,焦点是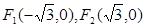 ,点
,点 到直线
到直线 的距离为
的距离为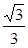 ,过点
,过点 且倾斜角为锐角的直线
且倾斜角为锐角的直线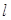 与椭圆交于A、B两点,使得
与椭圆交于A、B两点,使得 .
. 的距离为
的距离为 可知-
可知- +
+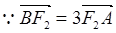 ,设出点A(x1,y1)、B(x2,y2).,借助于向量公式
,设出点A(x1,y1)、B(x2,y2).,借助于向量公式 再利用 A、B在椭圆
再利用 A、B在椭圆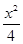 +y2=1上, 得到坐标的值,然后求解得到直线方程。
+y2=1上, 得到坐标的值,然后求解得到直线方程。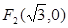
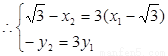
 ……10分
……10分 =
= .
.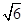 =0.
=0.