题目内容
| |||||||||||||||
解析:
(1) |
解析:(1)由已知.得S1=a1=1,S2=a1+a2=7,S3=a1+a2+a3=18. 由(5n-8)Sn+1-(5n+2)Sn=An+B知 解得A=-20,B=-8. |
(2) |
方法一 由(1)得,(5n-8)Sn+1-(5n+2)Sn=-20n-8 ①.所以(5n-3)Sn+2-(5n+7)Sn+l=-20n-28②. ②-①.得(5n-3)Sn+2-(10n-1)Sn+1+(5n+2)Sn=-20 ③.所以(5n+2)Sn+3-(10n+9)Sn+2+(5n+7)Sn+1=-20④. ④-③,得(5n+2)Sn+3-(15n+6)Sn+2+(15n+6)Sn+1-(5n+2)Sn=0. 因为an+1=Sn+l-Sn,所以(5n+2)an+3-(10n+4)an+2+(5n+2)an+1=0. 又因为5n+2≠0,所以an+3-2an+2+an+1=0, 即an+3-an+2=an+2-an+1,n≥1. 又a3-a2=a2-a1=5, 所以数列{an}为等差数列. 方法二 由已知.S1=a1=1, 又(5n-8)Sn+l-(5n+2)Sn=-20n-8,且5n-8≠0。 所以数列{Sn}是惟一确定的,因而数列{an}是惟一确定的. 设bn=5n-4,则数列{bn}为等差数列,前n项和Tn= 于是(5n-8)Tn+1-(5n+2)Tn=(5n-8) 由惟一性得bn=an,即数列{an}为等差数列. |
(3) |
由(2)可知,an=1+5(n-1)=5n-4. 要证 因为amn=5mn-4,aman=(5m-4)(5n-4)=25mn-20(m+n)+16, 故只要证5(5mn-4)>1+25mn-20(m+n)+16+2 因为2 点评:此高考题是一道数列与不等式的综合题,(1)、(2)两小题考生容易入手,第(3)小题采用了基本不等式、分析法、放缩法等证明技巧. |

 阅读快车系列答案
阅读快车系列答案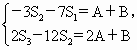 即
即