题目内容
 如图,已知曲线C1:y=x3(x≥0)与曲线C2:y=-2x3+3x(x≥0)交于O,A,直线x=t(0<t<1)与曲线C1,C2分别交于B,D.
如图,已知曲线C1:y=x3(x≥0)与曲线C2:y=-2x3+3x(x≥0)交于O,A,直线x=t(0<t<1)与曲线C1,C2分别交于B,D.(Ⅰ)写出四边形ABOD的面积S与t的函数关系式S=f(t);
(Ⅱ)讨论f(t)的单调性,并求f(t)的最大值.
分析:(Ⅰ)先求出两曲线的交点O、A坐标,由直线x=t(0<t<1)与曲线C1,C2分别交于B,D表示出BD的长,利用四边形ABOD的面积等于三角形ABO的面积+三角形OBD的面积;即可表示函数f(t)的关系式;
(Ⅱ)令f'(t)=0解得t,分区间讨论f(t)的增减性得到哦f(t)的最大值及此时t的值即可.
(Ⅱ)令f'(t)=0解得t,分区间讨论f(t)的增减性得到哦f(t)的最大值及此时t的值即可.
解答:解:(Ⅰ)由
得交点O、A的坐标分别是(0,0),(1,1).f(t)=S△ABO+S△OBD=
|BD|•|1-0|=
|BD|=
(-3t3+3t),
即f(t)=-
(t3-t),(0<t<1).
(Ⅱ)f′(t)=-
t2+
.令f'(t)=0解得t=
.
当0<t<
时,f′(t)>0,从而f(t)在区间(0,
)上是增函数;
当
<t<1时,f′(t)<0,从而f(t)在区间(
,1)上是减函数.
所以当t=
时,f(t)有最大值为f(
)=
.
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即f(t)=-
| 3 |
| 2 |
(Ⅱ)f′(t)=-
| 9 |
| 2 |
| 3 |
| 2 |
| ||
| 3 |
当0<t<
| ||
| 3 |
| ||
| 3 |
当
| ||
| 3 |
| ||
| 3 |
所以当t=
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
点评:考查学生根据实际问题选择函数关系的能力,以及利用导数研究函数增减性,利用导数求闭区间上函数最值的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
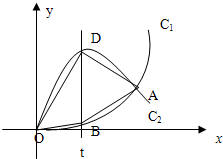 如图,已知曲线C1:y=x3(x≥0)与曲线C2:y=-2x3+3x(x≥0)交于O,A,直线x=
如图,已知曲线C1:y=x3(x≥0)与曲线C2:y=-2x3+3x(x≥0)交于O,A,直线x= (2007•广州一模)如图,已知曲线C1:y=x2与曲线C2:y=-x2+2ax(a>1)交于点O,A,直线x=t(0<t≤1)与曲线C1,C2分别相交于点D,B,连结OD,DA,AB,OB.
(2007•广州一模)如图,已知曲线C1:y=x2与曲线C2:y=-x2+2ax(a>1)交于点O,A,直线x=t(0<t≤1)与曲线C1,C2分别相交于点D,B,连结OD,DA,AB,OB. (2009•黄冈模拟)如图,已知曲线
(2009•黄冈模拟)如图,已知曲线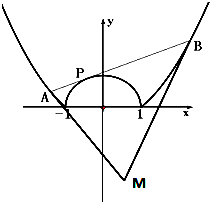 如图,已知曲线C1:x2+y2=1(|x|<1),C2:x2=8y+1(|x|≥1),动直线l与C1相切,与C2相交于A,B两点,曲线C2在A,B处的切线相交于点M.
如图,已知曲线C1:x2+y2=1(|x|<1),C2:x2=8y+1(|x|≥1),动直线l与C1相切,与C2相交于A,B两点,曲线C2在A,B处的切线相交于点M.