题目内容
若函数f(x)对于任意x∈[a,b],恒有|f(x)-f(a)-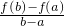 (x-a)|≤T(T为常数)成立,则称函数f(x)在[a,b]上具有“T级线性逼近”.下列函数中:
(x-a)|≤T(T为常数)成立,则称函数f(x)在[a,b]上具有“T级线性逼近”.下列函数中:
①f(x)=2x+1;
②f(x)=x2;
③f(x)= ;
;
④f(x)=x3.
则在区间[1,2]上具有“ 级线性逼近”的函数的个数为
级线性逼近”的函数的个数为
- A.1
- B.2
- C.3
- D.4
C
分析:根据称函数f(x)在[a,b]上具有“T级线性逼近”的定义,判断各个选项中的函数在区间[1,2]上是否满足“ 级线性逼近”的定义,从而得出结论.
级线性逼近”的定义,从而得出结论.
解答:f(x)=2x+1在区间[1,2]上,由于|f(x)-f(1)-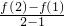 (x-1)|=|0|≤
(x-1)|=|0|≤ ,故f(x)=2x+1在区间[1,2]上具有“
,故f(x)=2x+1在区间[1,2]上具有“ 级线性逼近”,故满足条件.
级线性逼近”,故满足条件.
f(x)=x2 在区间[1,2]上,由于|f(x)-f(1)-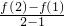 (x-1)|=|(x-1)(x-2)|=-(x-1)(x-2)≤
(x-1)|=|(x-1)(x-2)|=-(x-1)(x-2)≤ ,
,
故f(x)=x2在区间[1,2]上具有“ 级线性逼近”,故满足条件.
级线性逼近”,故满足条件.
f(x)= 在区间[1,2]上,由于|f(x)-f(1)-
在区间[1,2]上,由于|f(x)-f(1)-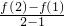 (x-1)|=|
(x-1)|=| +
+ -
- |=
|= -(
-( +
+ )≤
)≤ -2
-2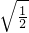 =
= -
- ≤
≤ ,
,
故f(x)=2x+1在区间[1,2]上具有“ 级线性逼近”,故满足条件.
级线性逼近”,故满足条件.
f(x)=x3在区间[1,2]上,由于|f(x)-f(1)-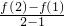 (x-1)|=|x3-7x+6|=|(x-1)(x-3)(x+2)|=-(x-1)(x-3)(x+2),
(x-1)|=|x3-7x+6|=|(x-1)(x-3)(x+2)|=-(x-1)(x-3)(x+2),
由于-(x3-7x+6)的导数为-3x2+7,令-3x2+7=0 可得 x=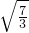 ,在[1,
,在[1,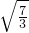 ]上,3x2-7<0,-(x-1)(x-3)(x+2)为增函数,
]上,3x2-7<0,-(x-1)(x-3)(x+2)为增函数,
同理可得在[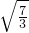 ,2]上,-(x-1)(x-3)(x+2)为减函数,故-(x-1)(x-3)(x+2)的最大值为 (
,2]上,-(x-1)(x-3)(x+2)为减函数,故-(x-1)(x-3)(x+2)的最大值为 (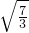 -1)(3-
-1)(3-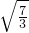 )(
)(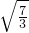 +2)>
+2)> ,
,
故不满足“ 级线性逼近”,故不满足条件.
级线性逼近”,故不满足条件.
故选C.
点评:本题主要考查新定义:“T级线性逼近”的定义,不等式的性质应用,式子的变形是解题的难点,属于中档题.
分析:根据称函数f(x)在[a,b]上具有“T级线性逼近”的定义,判断各个选项中的函数在区间[1,2]上是否满足“
 级线性逼近”的定义,从而得出结论.
级线性逼近”的定义,从而得出结论.解答:f(x)=2x+1在区间[1,2]上,由于|f(x)-f(1)-
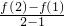 (x-1)|=|0|≤
(x-1)|=|0|≤ ,故f(x)=2x+1在区间[1,2]上具有“
,故f(x)=2x+1在区间[1,2]上具有“ 级线性逼近”,故满足条件.
级线性逼近”,故满足条件.f(x)=x2 在区间[1,2]上,由于|f(x)-f(1)-
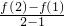 (x-1)|=|(x-1)(x-2)|=-(x-1)(x-2)≤
(x-1)|=|(x-1)(x-2)|=-(x-1)(x-2)≤ ,
,故f(x)=x2在区间[1,2]上具有“
 级线性逼近”,故满足条件.
级线性逼近”,故满足条件.f(x)=
 在区间[1,2]上,由于|f(x)-f(1)-
在区间[1,2]上,由于|f(x)-f(1)-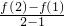 (x-1)|=|
(x-1)|=| +
+ -
- |=
|= -(
-( +
+ )≤
)≤ -2
-2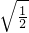 =
= -
- ≤
≤ ,
,故f(x)=2x+1在区间[1,2]上具有“
 级线性逼近”,故满足条件.
级线性逼近”,故满足条件.f(x)=x3在区间[1,2]上,由于|f(x)-f(1)-
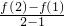 (x-1)|=|x3-7x+6|=|(x-1)(x-3)(x+2)|=-(x-1)(x-3)(x+2),
(x-1)|=|x3-7x+6|=|(x-1)(x-3)(x+2)|=-(x-1)(x-3)(x+2),由于-(x3-7x+6)的导数为-3x2+7,令-3x2+7=0 可得 x=
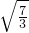 ,在[1,
,在[1,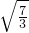 ]上,3x2-7<0,-(x-1)(x-3)(x+2)为增函数,
]上,3x2-7<0,-(x-1)(x-3)(x+2)为增函数,同理可得在[
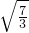 ,2]上,-(x-1)(x-3)(x+2)为减函数,故-(x-1)(x-3)(x+2)的最大值为 (
,2]上,-(x-1)(x-3)(x+2)为减函数,故-(x-1)(x-3)(x+2)的最大值为 (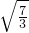 -1)(3-
-1)(3-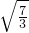 )(
)(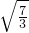 +2)>
+2)> ,
,故不满足“
 级线性逼近”,故不满足条件.
级线性逼近”,故不满足条件.故选C.
点评:本题主要考查新定义:“T级线性逼近”的定义,不等式的性质应用,式子的变形是解题的难点,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,3},则使函数y=xa的定义域为R且该函数为奇函数的所有a的值为1,3;
,3},则使函数y=xa的定义域为R且该函数为奇函数的所有a的值为1,3; )>
)> [f(x1)+f(x2)],则称f(x)为定义域上的凸函数.
[f(x1)+f(x2)],则称f(x)为定义域上的凸函数.