题目内容
下列四个命题中,正确的是
A.已知 服从正态分布 服从正态分布 , , ,且 ,且 ,则 ,则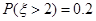 |
B.设回归直线方程为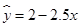 ,当变量 ,当变量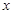 增加一个单位时, 增加一个单位时,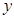 平均增加 平均增加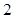 个单位; 个单位; |
C.已知函数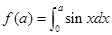 ,则 ,则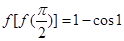 ; ; |
D.对于命题 : : ,使得 ,使得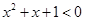 ,则 ,则 : :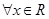 ,均有 ,均有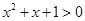 |
C
解析
由随机变量ξ服从正态分布N(0,σ2)可知正态密度曲线关于y轴对称,
而P(﹣2≤x≤0)=0.4,
∴P(﹣2≤x≤2)=0.8
则P(ξ>2)= (1﹣P(﹣2≤x≤2))=0.1,故A错.
(1﹣P(﹣2≤x≤2))=0.1,故A错.
B、回归方程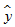 =2﹣2.5x,变量x增加一个单位时,
=2﹣2.5x,变量x增加一个单位时,
变量y平均变化[2﹣2.5(x+1)]﹣(2﹣2.5x)=﹣2.5
∴变量y平均减少2.5个单位,故B错误;
C、∵函数f(a)= ,∴f(
,∴f( )=
)= sinxdx=(﹣cosx)
sinxdx=(﹣cosx)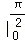 =0﹣(﹣1)=1;
=0﹣(﹣1)=1;
∴f[f( )]=f(1)=
)]=f(1)=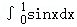 =(﹣cosx)
=(﹣cosx) =﹣cos1﹣(﹣cos0)=1﹣cos1;故C正确;
=﹣cos1﹣(﹣cos0)=1﹣cos1;故C正确;
D、对于命题p: ,使得x2+x+1<0,可得¬p:?x∈R,均有x2+x+1≥0,故D错误;
,使得x2+x+1<0,可得¬p:?x∈R,均有x2+x+1≥0,故D错误;
故选C;

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目