题目内容
已知向量
(1)当 时,求
时,求 的值;
的值;
(2)设函数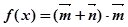 ,求
,求 的单调增区间;
的单调增区间;
(3)已知在锐角 中,
中, 分别为角
分别为角 的对边,
的对边, ,对于(2)中的函数
,对于(2)中的函数 ,求
,求 的取值范围。
的取值范围。
(1)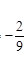 . (2)
. (2)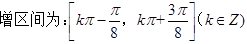 ,
,
(3)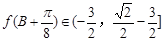 .
.
解析试题分析:(1)由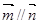 ,可得3sinx=-cosx,于是tanx=
,可得3sinx=-cosx,于是tanx=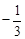 .
.
∴ 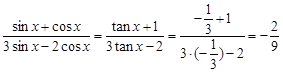 .
.
(2)∵ 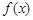 =
=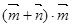
=(sinx+cosx,2)·(sinx,-1)
=sin2x+sinxcosx-2
=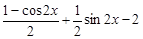
=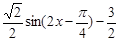 ,
, 
(无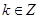 扣1分)
扣1分)
(3)∵在△ABC中,A+B=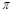 -C,于是
-C,于是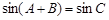 ,
,
由正弦定理知: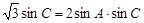 ,
,
∴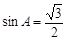 ,可解得
,可解得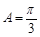 .
.
又△ABC为锐角三角形,于是 ,
,
∴ 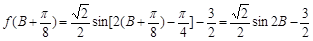 .
.
由 得
得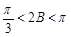 ,
,
∴ 0<sin2B≤1,得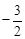 <
<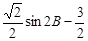 ≤
≤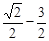 .
.
即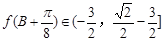 .
.
考点:本题主要考查平面向量的坐标运算,三角函数的同角公式、和差倍半公式,三角函数性质,正弦定理的应用。
点评:典型题,为研究三角函数的图象和性质,往往需要利用三角函数和差倍半公式将函数“化一”。本题由平面向量的坐标运算得到f(x)的表达式,通过“化一”,利用三角函数性质,求得周期、最小值。(3)则利用正弦定理,求得角A,进一步得到角B的范围,达到解题目的。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知D,E,F分别是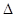 ABC的边AB,BC,CA的中点,则( ).
ABC的边AB,BC,CA的中点,则( ).
A.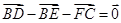 | B.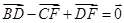 |
C.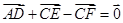 | D.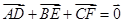 |

 及
及 ;
; 的值域;
的值域; ,若关于x的方程
,若关于x的方程 有两个不同的实数解,求实数
有两个不同的实数解,求实数 的取值范围.
的取值范围. 中,
中, 分别是角
分别是角 所对的边
所对的边
 ,
, ,函数
,函数 .
. 的最小正周期及单调增区间
的最小正周期及单调增区间 ,求
,求 中,
中,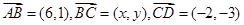 .
.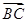 ∥
∥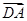 ,试求
,试求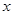 与
与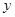 满足的关系
满足的关系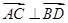 ,求
,求 =3i-4j,
=3i-4j, =6i-3j,
=6i-3j, =(5-m)i-(3+m)j其中i,j分别是直角坐标系内x轴与y轴正方向上的单位向量
=(5-m)i-(3+m)j其中i,j分别是直角坐标系内x轴与y轴正方向上的单位向量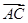 2≤-x2+x+3恒成立,求x的取值范围
2≤-x2+x+3恒成立,求x的取值范围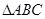 的角A、B、C所对的边分别是
的角A、B、C所对的边分别是 ,设向量
,设向量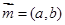 ,
, 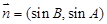 ,
, 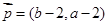
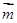 ∥
∥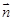 ,求证:
,求证: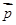 ,边长
,边长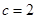 ,
,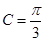 ,求
,求