题目内容
已知函数 .
.
(1)求证: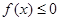 ;
;
(2)若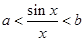 对
对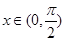 恒成立,求
恒成立,求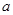 的最大值与
的最大值与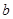 的最小值.
的最小值.
(1)详见解析;(2)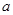 的最大值为
的最大值为 ,
,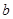 的最小值为1.
的最小值为1.
解析试题分析:(1)求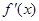 ,由
,由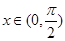 ,判断出
,判断出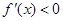 ,得出函数
,得出函数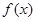 在
在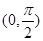 上单调递减,从而
上单调递减,从而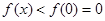 ;(2)由于
;(2)由于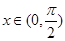 ,“
,“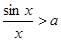 ”等价于“
”等价于“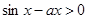 ”,“
”,“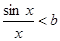 ”等价于“
”等价于“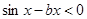 ”,令
”,令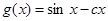 ,则
,则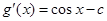 ,对
,对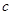 分
分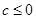 ;
;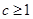 ;
;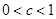 进行讨论,
进行讨论,
用导数法判断函数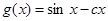 的单调性,从而确定当
的单调性,从而确定当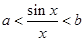 对
对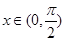 恒成立时
恒成立时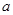 的最大值与
的最大值与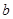 的最小值.
的最小值.
(1)由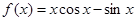 得
得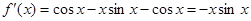 ,
,
因为在区间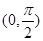 上
上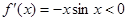 ,所以,
,所以,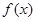 在区间
在区间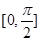 上单调递减,
上单调递减,
从而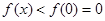 .
.
(2)当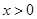 时,“
时,“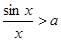 ”等价于“
”等价于“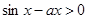 ”,“
”,“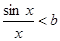 ”等价于“
”等价于“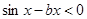 ”,
”,
令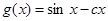 ,则
,则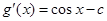 ,
,
当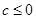 时,
时, 对任意
对任意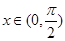 恒成立,
恒成立,
当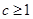 时,因为对任意
时,因为对任意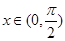 ,
,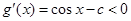 ,所以
,所以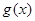 在区间
在区间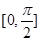 上单调递减,从而
上单调递减,从而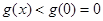 对任意
对任意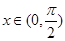 恒成立.
恒成立.
当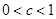 时 ,存在唯一的
时 ,存在唯一的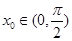 使得
使得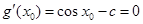 ,
,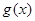 、
、 在区间
在区间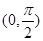 上的情况如下表:
上的情况如下表: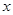
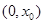
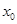
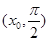

 练习册系列答案
练习册系列答案
桂壮红皮书应用题卡系列答案
快乐过暑假系列答案
同步练习册全优达标测试卷系列答案
英才教程探究习案课时精练系列答案

初中语文阅读轻松组合周周练系列答案

剑桥小学英语系列答案
作业本江西教育出版社系列答案
新起点百分百单元测试卷系列答案
相关题目
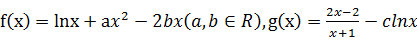 .
.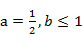 时,
时,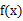 与
与 )在定义域上单调性相反,求的
)在定义域上单调性相反,求的 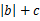 的最小值。
的最小值。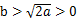 时,求证:存在
时,求证:存在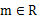 ,使
,使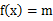 的三个不同的实数解
的三个不同的实数解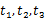 ,且对任意
,且对任意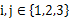 且
且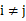 都有
都有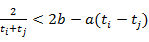 .
. ,其中
,其中
 在其定义域上的单调性;
在其定义域上的单调性; 时,求
时,求 的值.
的值.
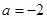 ,求证:函数
,求证:函数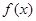 在(1,+∞)上是增函数;
在(1,+∞)上是增函数;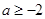 时,求函数
时,求函数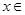 [l,e],使得
[l,e],使得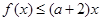 成立,求实数
成立,求实数 的取值范围.
的取值范围. 为常数,e=2.71828…是自然对数的底数),曲线
为常数,e=2.71828…是自然对数的底数),曲线 在点
在点 处的切线与x轴平行.
处的切线与x轴平行. 的单调区间;
的单调区间; ,其中
,其中 为
为 .
.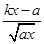 -ln a(x>0,a>0且为常数).
-ln a(x>0,a>0且为常数).