题目内容
设向量

 ,函数
,函数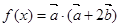 .
.
(1)求函数 的单调递增区间;
的单调递增区间;
(2)求使不等式 成立的
成立的 的取值集合.
的取值集合.
【答案】
(1)
 ;(2)
;(2) .
.
【解析】
试题分析:(1)本题用向量给出条件,因此首先我们把 求出来,利用向量的数量积运算,可得
求出来,利用向量的数量积运算,可得 ,然后我们三角函数化为
,然后我们三角函数化为 的形式,再利用正弦函数的性质解题,在变形过程中,注意使
的形式,再利用正弦函数的性质解题,在变形过程中,注意使 .在
.在 都大于0的情况下,
都大于0的情况下,
 的单调增区间只要解不等式
的单调增区间只要解不等式 即得.(2)不等式
即得.(2)不等式 是一个三角不等式,因
是一个三角不等式,因 ,同样只要利用余弦函数的性质即可.
,同样只要利用余弦函数的性质即可.
试题解析:(1)


 . 5′
. 5′
由 ,得
,得
 ,
,
∴ 的单调递增区间为
的单调递增区间为
 . 8′
. 8′
(2)由 ,得
,得 .
.
由 ,得
,得 ,则
,则 ,
,
即
 . ∴使不等式
. ∴使不等式 成立的
成立的 的取值集合为
的取值集合为 . 14′
. 14′
考点:(1)向量的数量积与三角函数的单调性;(2)复合函数的导数与余弦函数的性质.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
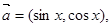

 ,函数
,函数 .
. 的单调递增区间;
的单调递增区间; 成立的
成立的 的取值集合.
的取值集合. ,
, ,
, .
. ,求x的值;
,求x的值; ,求f(x)的最大值.
,求f(x)的最大值.