题目内容
直线 与函数
与函数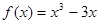 的图像有相异的三个公共点,则
的图像有相异的三个公共点,则 的取值范围是
的取值范围是
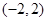
解析试题分析:结合函数图象,a介于f(x)的极大值和极小值之间。
因为, =x3-3x ,所以,f’(x)=3x²-3,令f'(x)=0,得:x=-1,x=1
=x3-3x ,所以,f’(x)=3x²-3,令f'(x)=0,得:x=-1,x=1
f(-1)=2,f(1)=-2
所以,-2<a<2,故答案为(-2,2)。
考点:数形结合思想,转化与化归思想,利用导数研究函数的极值。
点评:简单题,利用数形结合法,将问题转化成利用导数研究函数的极值。

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
 与函数
与函数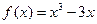 的图像有相异的三个公共点,则
的图像有相异的三个公共点,则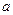 的取值范围是 。
的取值范围是 。 与函数
与函数 的图像有相异的三个公共点,则
的图像有相异的三个公共点,则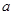 的取值范围是
的取值范围是 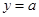 与函数
与函数 的图像有相异的三个公共点,则
的图像有相异的三个公共点,则 的取值范围是
;
的取值范围是
; 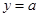 与函数
与函数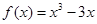 的图像有相异的三个公共点,则
的图像有相异的三个公共点,则 的取值范围是
。
的取值范围是
。