题目内容
设
，
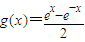，计算可知 f（1）g（3）+g（1）f（3）-g（4）=0，f（3）g（2）+g（3）f（2）-g（5）=0，并由此概括出关于函数f（x）和g（x）的一个等式，使上面的两个等式是你写出的等式的特例，这个等式是 ．
【答案】分析：由已知中函数的解析式及f（1）g（3）+g（1）f（3）-g（4）=0，f（3）g（2）+g（3）f（2）-g（5）=0，分析两个式子中自变量之间的关系，归纳推理可得答案．
解答：解：∵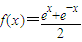
，
，
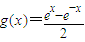且f（1）g（3）+g（1）f（3）-g（4）=0，
f（3）g（2）+g（3）f（2）-g（5）=0，
…
归纳可得：
f（a）g（b）+f（b）g（a）-g（a+b）=0
故答案为：f（a）g（b）+f（b）g（a）-g（a+b）=0
点评：本题考查的知识点是归纳推理，其中根据已知分析出等式中变量之间的关系规律是解答的关键．
解答：解：∵
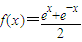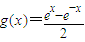，，且f（1）g（3）+g（1）f（3）-g（4）=0，
f（3）g（2）+g（3）f（2）-g（5）=0，
…
归纳可得：
f（a）g（b）+f（b）g（a）-g（a+b）=0
故答案为：f（a）g（b）+f（b）g（a）-g（a+b）=0
点评：本题考查的知识点是归纳推理，其中根据已知分析出等式中变量之间的关系规律是解答的关键．
练习册系列答案
口算题天天练系列答案
相关题目
，
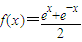，计算可知 f（1）g（3）+g（1）f（3）-g（4）=0，f（3）g（2）+g（3）f（2）-g（5）=0，并由此概括出关于函数f（x）和g（x）的一个等式，使上面的两个等式是你写出的等式的特例，这个等式是 ．