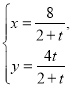题目内容
【题目】设常数![]() ,函数
,函数![]() .
.
(1)令![]() 时,求
时,求![]() 的最小值,并比较
的最小值,并比较![]() 的最小值与零的大小;
的最小值与零的大小;
(2)求证:![]() 在
在![]() 上是增函数;
上是增函数;
(3)求证:当![]() 时,恒有
时,恒有![]() .
.
【答案】(1)最小值为![]() ,最小值大于零.(2)证明见解析.(3)证明见解析
,最小值大于零.(2)证明见解析.(3)证明见解析
【解析】
(1)对函数![]() 进行求导,确定函数
进行求导,确定函数![]() 的解析式,再对函数
的解析式,再对函数![]() 求导,列表判断出该函数的单调性以及极值,最后确定函数
求导,列表判断出该函数的单调性以及极值,最后确定函数![]() 的最小值,再判断
的最小值,再判断![]() 的最小值与零的大小即可;
的最小值与零的大小即可;
(2)利用(1)中的结论,可以判断出函数![]() 的正负性,进而能证明出
的正负性,进而能证明出![]() 的单调性;
的单调性;
(3)利用(2)中的结论进行证明即可.
(1)因为![]() ,
,
所以![]() .
.
所以![]() ,
,
所以![]() ,令
,令![]() ,得
,得![]() .
.
列表如下:
|
| 2 |
|
|
| 0 |
|
| 减 | 极小值 | 增 |
所以![]() 在
在![]() 处取得极小值
处取得极小值![]() ,
,
即![]() 的最小值为
的最小值为![]() ,
,
因为![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() 即
即![]() 的最小值大于零.
的最小值大于零.
(2)由(1)知,![]() 的最小值为正数,
的最小值为正数,
所以对一切![]() ,恒有
,恒有![]() .
.
从而当![]() 时,恒有
时,恒有![]() ,故
,故![]() 在
在![]() 上是增函数.
上是增函数.
(3)由(2)知![]() 在
在![]() 上是增函数,
上是增函数,
所以当![]() 时,
时,![]() .
.
又![]() ,
,
所以![]() ,即
,即![]() ,
,
所以![]() ,
,
故当![]() 时,恒有
时,恒有![]() .
.

练习册系列答案
相关题目
【题目】雅山中学采取分层抽样的方法从应届高三学生中按照性别抽出20名学生作为样本,其选报文科理科的情况如下表所示.
男 | 女 | |
文科 | 2 | 5 |
理科 | 10 | 3 |
(Ⅰ)若在该样本中从报考文科的学生中随机地选出3人召开座谈会,试求3人中既有男生也有女生的概率;
(Ⅱ)用假设检验的方法分析有多大的把握认为雅山中学的高三学生选报文理科与性别有关?
参考公式和数据:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.07 | 2.71 | 3.84 | 5.02 | 6.64 | 7.88 | 10.83 |