题目内容
16.正方体ABCD-A1B1C1D1的棱长为1,E为BB1的中点,F为AD的中点,以DA,DC,DD1为x轴、y轴、z轴建立空间直角坐标系,设平面D1EF的法向量为(ak,bk,ck)(k≠0),则平面D1EF的法向量是(4k,-3k,2k)(k≠0).分析 求出各个点的坐标,进而求出向量$\overrightarrow{{D}_{1}E}$,$\overrightarrow{{D}_{1}F}$的坐标,结合$\left\{\begin{array}{l}\overrightarrow{m}•\overrightarrow{{D}_{1}E}=0\\ \overrightarrow{m}•\overrightarrow{{D}_{1}F}=0\end{array}\right.$,即$\left\{\begin{array}{l}ak+bk-\frac{1}{2}ck=0\\ \frac{1}{2}ak-ck=0\end{array}\right.$,可得答案.
解答 解:如下图所示:
∵正方体ABCD-A1B1C1D1的棱长为1,E为BB1的中点,F为AD的中点,
∴D1(0,0,1),E(1,1,$\frac{1}{2}$),F($\frac{1}{2}$,0,0),
则$\overrightarrow{{D}_{1}E}$=(1,1,-$\frac{1}{2}$),$\overrightarrow{{D}_{1}F}$=($\frac{1}{2}$,0,-1),
设平面D1EF的法向量为$\overrightarrow{m}$=(ak,bk,ck)(k≠0),
则$\left\{\begin{array}{l}\overrightarrow{m}•\overrightarrow{{D}_{1}E}=0\\ \overrightarrow{m}•\overrightarrow{{D}_{1}F}=0\end{array}\right.$,即$\left\{\begin{array}{l}ak+bk-\frac{1}{2}ck=0\\ \frac{1}{2}ak-ck=0\end{array}\right.$,
令c=2,则a=4,b=-3,
故平面D1EF的法向量是(4k,-3k,2k),
故答案为:(4k,-3k,2k)(k≠0)
点评 本题考查的知识点是平面的法向量,熟练掌握平面法向量的求法,是解答的关键.

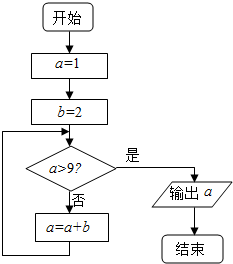 如图所示的程序框图,运行相应的程序,则输出a的值为( )
如图所示的程序框图,运行相应的程序,则输出a的值为( )| A. | 7 | B. | 9 | C. | 11 | D. | 13 |