题目内容
如图所示,已知直线![]() 的斜率为
的斜率为![]() 且过点
且过点![]() ,抛物线
,抛物线![]()
![]() , 直线与抛物线
, 直线与抛物线![]() 有两个不同的交点,
有两个不同的交点, ![]() 是抛物线的焦点,点
是抛物线的焦点,点![]() 为抛物线内一定点,点
为抛物线内一定点,点![]() 为抛物线上一动点.
为抛物线上一动点.
(1)求![]() 的最小值;
的最小值;
(2)求![]() 的取值范围;
的取值范围;
(3)若![]() 为坐标原点,问是否存在点
为坐标原点,问是否存在点![]() ,使过点
,使过点![]() 的动直线与抛物线交于
的动直线与抛物线交于![]() 两点,且以
两点,且以![]() 为直径的圆恰过坐标原点, 若存在,求出动点
为直径的圆恰过坐标原点, 若存在,求出动点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

解:如图,设抛物线的准线为![]() , 过
, 过![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,
,
(1)由抛物线定义知![]()
![]() (折线段大于垂线段),当且仅当
(折线段大于垂线段),当且仅当![]() 三点共线取等号.由题意知
三点共线取等号.由题意知![]() ,即
,即
![]() 的最小值是8………...4分
的最小值是8………...4分
(2) ![]() ……...5分
……...5分
(3)假设存在点![]() ,设过点
,设过点![]() 的直线方程为
的直线方程为![]() ,
,
显然![]() ,
,![]() ,设
,设![]() ,
,![]() ,由以
,由以![]() 为直径的圆恰过坐标
为直径的圆恰过坐标
原点有![]()
![]()
![]() ………… ……………………...①……9分
………… ……………………...①……9分
把![]() 代人
代人![]() 得
得![]() 由韦达定理
由韦达定理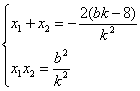 ………………….………………②
………………….………………②
又 ![]() ….③
….③
②代人③得![]()
![]() ……… .④
……… .④
②④代人①得![]() … …12分
… …12分
![]() 动直线方程为
动直线方程为![]() 必过定点
必过定点![]()
当![]() 不存在时,直线
不存在时,直线![]() 交抛物线于
交抛物线于![]() ,仍然有
,仍然有![]() , 综上:存在点
, 综上:存在点![]()
![]() 满足条件……………15分
满足条件……………15分


练习册系列答案
相关题目
 如图所示,已知直线l:3x+4y-12=0与x,y轴的正半轴分别交于A,B两点,直线l1和AB,OA分别交于C,D,且平分△AOB的面积,求CD的最小值.
如图所示,已知直线l:3x+4y-12=0与x,y轴的正半轴分别交于A,B两点,直线l1和AB,OA分别交于C,D,且平分△AOB的面积,求CD的最小值.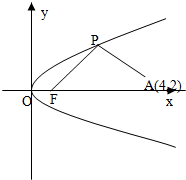 如图所示,已知直线l的斜率为k且过点Q(-3,0),抛物线C:y2=16x,直线与抛物线l有两个不同的交点,F是抛物线的焦点,点A(4,2)为抛物线内一定点,点P为抛物线上一动点.
如图所示,已知直线l的斜率为k且过点Q(-3,0),抛物线C:y2=16x,直线与抛物线l有两个不同的交点,F是抛物线的焦点,点A(4,2)为抛物线内一定点,点P为抛物线上一动点.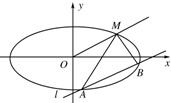 如图所示,已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的3倍且经过点M(3,1).平行于OM的直线l在y轴上的截距为m(m≠0),且交椭圆于A,B两不同点.
如图所示,已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的3倍且经过点M(3,1).平行于OM的直线l在y轴上的截距为m(m≠0),且交椭圆于A,B两不同点. 的斜率为
的斜率为 且过点
且过点 ,抛物线
,抛物线
 , 直线与抛物线
, 直线与抛物线 是抛物线的焦点,点
是抛物线的焦点,点 为抛物线内一定点,点
为抛物线内一定点,点 为抛物线上一动点.
为抛物线上一动点. 的最小值;
的最小值; 为坐标原点,问是否存在点
为坐标原点,问是否存在点 ,使过点
,使过点 两点,且以
两点,且以 为直径的圆恰过坐标原点, 若存在,求出动点
为直径的圆恰过坐标原点, 若存在,求出动点