Question

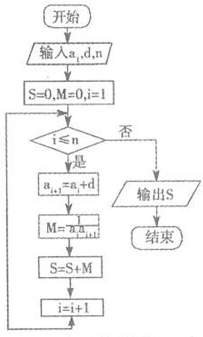已知等差数列{a_n}的各项均为正数，观察程序框图：若n=3时，S=

3

7

；n=9时，S=

9

19

，则数列的通项公式为（　　）

A．2n-1

B．2n

C．2n+1

D．2n+2

Answer 1

分析：由框图所示S=S+

1

aiai+1

可得S=

1

a1a1

+

1

a2a3

+…+

1

anan+1

，利用裂项可求和=

1

d

(

1

a1

-

1

an+1

)，由n=3，S=

1

d

(

1

a1

-

1

a4

)=

3

7

，n=9，S=

1

d

( 

1

a1

 -

1

a10

)=

9

19

，结合选项可知公差d=2，可求通项公式

解答：解：由框图所示S=S+

1

aiai+1

可得
S=

1

a1a1

+

1

a2a3

+…+

1

anan+1

=

1

d

(

1

a1

-

1

a2

+

1

a2

-

1

a3

+…+

1

an

-

1

an+1

)
=

1

d

(

1

a1

-

1

an+1

)
∵n=3，S=

1

d

(

1

a1

-

1

a4

)=

3

7

n=9，S=

1

d

( 

1

a1

 -

1

a10

)=

9

19

两式相减可得，

1

a4

-

1

a10

=(

9

19

-

3

7

)d
∴

6d

a4a10

=(

9

19

-

3

7

)d，结合选项可知公差d=2，
∴a₄=7，a₁₀=19
∴a_n=a₄+（n-4）×2=2n-1
故选：A

点评：本题主要考查了利用框图给出数列的和的递推公式，裂项法求数列的和，等差数列通项公式的应用，属于知识的简单综合运用．