题目内容
根据所给条件求直线的方程．
(1)直线过点(－4，0)，倾斜角的正弦值为
；(2)直线过点(－3，4)，且在两坐标轴上的截距之和为12；
(3)直线过点(5，10)，且到原点的距离为5．
答案：
解析：
解析：
|
解答 (1)由题设知，该直线的斜率存在，故可采用点斜式． 设倾斜角为α，则sinα＝ 从而cosα＝± 则k＝tanα＝± 故所求直线方程为：y＝± (2)由题设知截距不为0，设直线方程为 从而 故所求直线方程为：4x－y＋16＝0或x＋3y－9＝0． (3)依题设知，此直线有斜率不存在的情况． 当斜率不存在时，所求直线方程为：x－5＝0； 当斜率存在时，设其为k，则y－10＝k(x－5)， 即kx－y＋(10－5k)＝0． 由点线距离公式，得 解得k＝ 故所求直线方程为3x－4y＋25＝0． 综上知，所求直线方程为x－5＝0或3x－4y＋25＝0． 评析 求直线方程时，一方面应依据题设条件灵活选取方程的形式，另一方面应特别注意直线方程各种形式的适用范围，即注意分类讨论． |
(0＜α＜π)，
，
．
(x＋4)．
＋
＝1，
＋
＝1，解得a＝－4成9．
＝5，
．
练习册系列答案
相关题目
．求动点P的轨迹方程．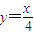
上的点，点列A1（x1，0），A2（x2，0），…，An（xn，0），…（n∈N*）顺次为x轴上的点，其中x1=a（0＜a＜1），对任意的n∈N*，点An、Bn、An+1构成以Bn为顶点的等腰三角形．