题目内容
下列命题中,真命题是( )
分析:在正方体中举出反例加以证明,可得A不正确;根据面面垂直的性质定理,可得B不正确;根据平面与平面平行的性质,举出反例可得C不正确;根据垂直于同一条直线的直线与平面的位置关系,可得D正确.
解答:解:对于A,设m、n是正方体上底面内的两条相交直线,而平面α是正方体的下底面,
则m、n都平行于平面α,但是m与n不平行,因此A不正确;
对于B,由于α-l-β是直二面角,若m?α且m⊥l,则m⊥β,
但是条件中缺少了“m?α”,故不能得到“m⊥β”,因此B不正确;
对于C,若平面α∥β∥γ,m、n是分别位于β、γ内的异面直线,
则m∥平面α且n∥平面α,故C不正确;
对于D,由于直线m在平面α内的射影是一个点,所以直线m⊥α;.
又因为m⊥n,所以直线n与平面α平行或直线n在平面α内,因此D正确.
故选:D
则m、n都平行于平面α,但是m与n不平行,因此A不正确;
对于B,由于α-l-β是直二面角,若m?α且m⊥l,则m⊥β,
但是条件中缺少了“m?α”,故不能得到“m⊥β”,因此B不正确;
对于C,若平面α∥β∥γ,m、n是分别位于β、γ内的异面直线,
则m∥平面α且n∥平面α,故C不正确;
对于D,由于直线m在平面α内的射影是一个点,所以直线m⊥α;.
又因为m⊥n,所以直线n与平面α平行或直线n在平面α内,因此D正确.
故选:D
点评:本题给出空间线面平行、垂直位置关系的几个命题,要求我们找出其中的真命题.着重考查了线面平行、面面平行的判定与性质和面面垂直、线面垂直的判定与性质等知识,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
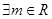 ,使函数
,使函数 是偶函数
是偶函数 ,使函数
,使函数 ≤0
≤0 =-1
=-1