题目内容
11.已知函数f(x)=2cos$\frac{ωx}{2}$($\sqrt{3}$cos$\frac{ωx}{2}$-sin$\frac{ωx}{x}$)(ω>0)的最小正周期为2π.(1)求函数f(x)的表达式;
(2)设θ∈(0,$\frac{π}{2}$),且f(θ)=$\sqrt{3}$+$\frac{6}{5}$,求cosθ的值.
分析 (1)把已知的函数解析式变形,结合其最小正周期求出ω,则函数解析式可求;
(2)把f(θ)=$\sqrt{3}$+$\frac{6}{5}$代入函数解析式求得$sin(θ-\frac{π}{3})=-\frac{3}{5}$,结合θ的范围得到cos($θ-\frac{π}{3}$),再由cosθ=cos[$(θ-\frac{π}{3})+\frac{π}{3}$]展开两角和的余弦得答案.
解答 解:(1)f(x)=2cos$\frac{ωx}{2}$($\sqrt{3}$cos$\frac{ωx}{2}$-sin$\frac{ωx}{x}$)
=$2\sqrt{3}co{s}^{2}\frac{ωx}{2}-2sin\frac{ωx}{2}cos\frac{ωx}{2}$
=$\sqrt{3}(1+cosωx)-sinωx$
=$\sqrt{3}+\sqrt{3}cosωx-sinωx$
=$\sqrt{3}-2sin(ωx-\frac{π}{3})$.
∵f(x)的最小正周期为2π,∴ω=1,
∴f(x)=$\sqrt{3}-2sin(x-\frac{π}{3})$;
(2)f(θ)=$\sqrt{3}-2sin(θ-\frac{π}{3})$=$\sqrt{3}$+$\frac{6}{5}$,
∴$sin(θ-\frac{π}{3})=-\frac{3}{5}$,
∵θ∈(0,$\frac{π}{2}$),∴$θ-\frac{π}{3}∈$($-\frac{π}{3},\frac{π}{6}$),
则cos($θ-\frac{π}{3}$)=$\frac{4}{5}$.
则cosθ=cos[$(θ-\frac{π}{3})+\frac{π}{3}$]=cos($θ-\frac{π}{3}$)cos$\frac{π}{3}$-sin($θ-\frac{π}{3}$)sin$\frac{π}{3}$
=$\frac{4}{5}×\frac{1}{2}-(-\frac{3}{5})×\frac{\sqrt{3}}{2}$=$\frac{4+3\sqrt{3}}{10}$.
点评 本题考查正弦函数的图象和性质,考查了三角恒等变换中的应用,是基础的计算题.

| A. | (0,2) | B. | (0,2] | C. | [0,2] | D. | (0,+∞) |
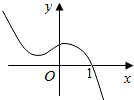 已知函数y=f(x)的图象如图,则满足$f({\frac{{2{x^2}-x-1}}{{{x^2}-2x+1}}^{\;}})•f(2)≤0$的x的取值范围[-2,1).
已知函数y=f(x)的图象如图,则满足$f({\frac{{2{x^2}-x-1}}{{{x^2}-2x+1}}^{\;}})•f(2)≤0$的x的取值范围[-2,1).