Question

已知数列{log₂(a_n－1)}（n∈N^＊）为等差数列，且a₁＝3，a₂＝5，则

　　＝

　　A、2　       　B、　　        C、1　　        D、

Answer 1

C

 

解析：∵{log₂（a_n－1）}（n∈N^*）为等差数列，

∴log₂（a_n－1）－log₂（a _n－1－1）=d（公差），

∴d=log₂（a₂－1）－log₂（a₁－1）

=log₂4－log₂2=1.

 

从而log₂=1（n≥2），

 

∴a_n－1=2（a_n－1－1），

 

∴=2（n≥2），

 

∴{a_n－1}为等比数列，公比q=2，

∴（++…+）

=［++…+］

=（++…+）

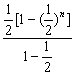==1.