题目内容
(选做题)(几何证明选讲)如图所示,过圆C外一点P做一条直线与圆C交于A,B两点,BA=2AP,PT与圆C相切于T点.已知圆C的半径为2,∠CAB=30°,则PT= .
3
解析试题分析:由已知中圆C的半径为2,∠CAB=30°,我们要以求出AB的长,又由过圆C外一点P做一条直线与圆C交于A,B两点,BA=2AP,我们可以进一步求出PA,PB长,结合已知中PT与圆C相切于T点和切割线定理,我们即可求出出线段PT的长
∵圆C的半径为2,∠CAB=30°,
∴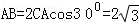 ,
,
又∵BA=2AP,
∴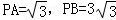 ,
,
又∵PT与圆C相切于T点.
由切割线定理可得:
PT2=PA•PB=9,
∴PT=3
考点:圆的切线的性质定理的证明
点评:本题考查的知识点是与圆有关的比例线段,其中根据已知条件计算出PA,PB长,为使用切割线定理,创造使用条件是解答本题的关键

练习册系列答案
相关题目
 ,当竹竿滑动到A1B1位置时,
,当竹竿滑动到A1B1位置时, ,竹竿在滑动时中点T也沿着某种轨迹运动到T1点,则T运动的路程是_________米.
,竹竿在滑动时中点T也沿着某种轨迹运动到T1点,则T运动的路程是_________米.
 的直线l将圆C:(x-2)2+y2=4分成两段弧,当劣弧所对
的直线l将圆C:(x-2)2+y2=4分成两段弧,当劣弧所对 的圆心角最小时,直线l的斜率k= ▲
的圆心角最小时,直线l的斜率k= ▲  外一点
外一点 做一条直线与圆
做一条直线与圆 两点,
两点, ,
, 与圆
与圆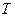 点.已知圆
点.已知圆 ,
, ,则
,则 _____.
_____. 
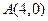 的直线
的直线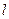 与曲线
与曲线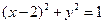 有公共点,则直线
有公共点,则直线 外切,同时与圆
外切,同时与圆 内切,求动圆圆心
内切,求动圆圆心 的轨迹方程
的轨迹方程 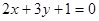 和圆
和圆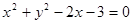 相交于点A、B,则弦AB的垂直平分线方程是. .
相交于点A、B,则弦AB的垂直平分线方程是. . 与圆
与圆 的公共弦长为
的公共弦长为 ,a=_______
,a=_______ 满足
满足 ,则
,则 的最小值为 。
的最小值为 。