题目内容
请先阅读:

(Ⅰ)利用上述想法(或其他方法),结合等式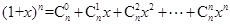 (
(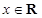 ,整数
,整数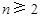 ),证明:
),证明: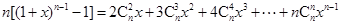 ;
;
(Ⅱ)当整数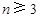 时,求
时,求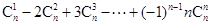 的值;
的值;
(Ⅲ)当整数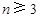 时,证明:
时,证明: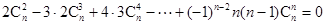 .
.

(Ⅰ)利用上述想法(或其他方法),结合等式
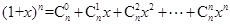 (
(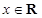 ,整数
,整数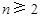 ),证明:
),证明: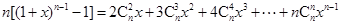 ;
;(Ⅱ)当整数
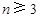 时,求
时,求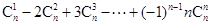 的值;
的值;(Ⅲ)当整数
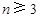 时,证明:
时,证明: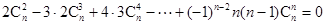 .
.(Ⅰ)证明:在等式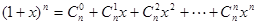 两边对x求导,
两边对x求导,
得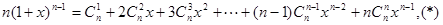 2分
2分
移项得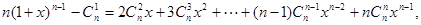
即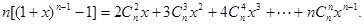 4分
4分
(Ⅱ)解:在(*)式中,令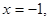
得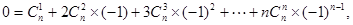
即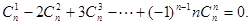 9分
9分
(Ⅲ)证明:由(Ⅰ)知
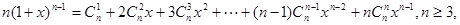 两边对x求导得
两边对x求导得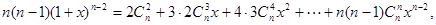 12分
12分
在上式中,令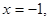
得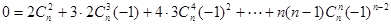 ,
,
即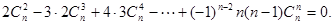 14分
14分
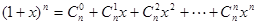 两边对x求导,
两边对x求导,得
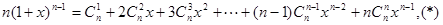 2分
2分移项得
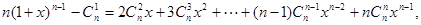
即
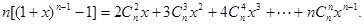 4分
4分(Ⅱ)解:在(*)式中,令
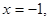
得
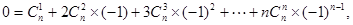
即
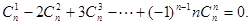 9分
9分(Ⅲ)证明:由(Ⅰ)知
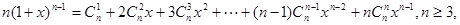 两边对x求导得
两边对x求导得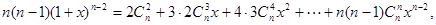 12分
12分在上式中,令
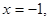
得
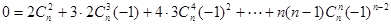 ,
,即
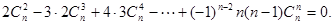 14分
14分本试题主要是考查了二项式定理的运用,以及系数和的求解的综合运用。
(1)利用二项式定理的 逆用可知表示所求解的结论。
(2)令x=-1,那么代入关系式中得到系数和。
(3)根据1中的结论可知,两边求解导数,然后对x=-1赋值得到结论。
(1)利用二项式定理的 逆用可知表示所求解的结论。
(2)令x=-1,那么代入关系式中得到系数和。
(3)根据1中的结论可知,两边求解导数,然后对x=-1赋值得到结论。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
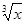 -
-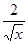 )15的展开式中:(1)常数项;(2)有几个有理项;(3)有几个整式项.
)15的展开式中:(1)常数项;(2)有几个有理项;(3)有几个整式项. 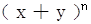 的展开式中,第七项的二项式系数最大,则n的值可能等于( )
的展开式中,第七项的二项式系数最大,则n的值可能等于( )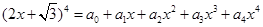 ,则
,则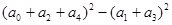 的值为 .
的值为 .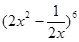 的二项展开式中的第四项的系数为
的二项展开式中的第四项的系数为 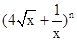 的展开式中各项系数之和为125,则展开式中的常数项为
的展开式中各项系数之和为125,则展开式中的常数项为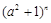 的展开式中各项系数之和等于
的展开式中各项系数之和等于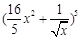 的展开式的常数项,并且
的展开式的常数项,并且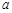 的值.
的值.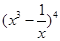 展开式中常数项为
展开式中常数项为 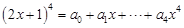 ,则
,则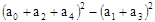 的值为__________.
的值为__________.