题目内容
某几何体的三视图如图所示,图中的四边形都是边长为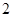 的正方形,两条虚线互相垂直,则该几何体的体积是( )
的正方形,两条虚线互相垂直,则该几何体的体积是( )
A. | B. | C. | D. |
A
解析试题分析:由三视图知:原几何体为一个棱长为2的正方体,里面挖去一个四棱锥,四棱锥的高为1.所以该几何体的体积为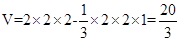 。
。
考点:三视图。
点评:做此类题的关键是正确还原几何体及几何体的一些棱的长。属于基础题型。

练习册系列答案
相关题目
(理)球O与锐二面角α-l-β的两半平面相切,两切点间的距离为,O点到交线l的距离为2,则球O的表面积为( )
| A. | B.4π | C.12π | D.36π |
一个棱锥的三视图如图,则该棱锥的表面积(单位:c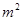 )为( )
)为( )
A.48+12 | B.48+24 | C.36+12 | D.36+24 |
圆锥母线长为1,侧面展开图的圆心角为240°,则圆锥体积为( )
A. | B. | C. | D. |
如图,正方体 的棱长为1,线段
的棱长为1,线段 上有两个动点E,F,且
上有两个动点E,F,且 ,则下列结论中错误的是 ( )
,则下列结论中错误的是 ( )
A. |
B. |
C.三棱锥 的体积为定值 的体积为定值 |
D.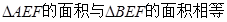 |
若三棱锥的一条棱长为 ,其余棱长均为1,体积是
,其余棱长均为1,体积是 ,则函数
,则函数 在其定义域上为( )
在其定义域上为( )
| A.增函数且有最大值 | B.增函数且没有最大值 |
| C.不是增函数且有最大值 | D.不是增函数且没有最大值 |
从点 出发的三条射线
出发的三条射线 两两成
两两成 角,且分别与球
角,且分别与球 相切于
相切于 三点,若球的体积为
三点,若球的体积为 ,则
,则 两点之间的距离为( )
两点之间的距离为( )
A. | B. | C.1.5 | D.2 |
 和直线
和直线 ,
, 所围成的平面图形,绕
所围成的平面图形,绕 轴旋转一周所得到的旋转体为
轴旋转一周所得到的旋转体为 ;由同时满足
;由同时满足 ,
, ,
, ,
, 的点
的点 构成的平面图形,绕
构成的平面图形,绕 .根据祖暅原理等知识,通过考察
.根据祖暅原理等知识,通过考察





 B.
B. C.
C.  D.
D. 