题目内容
线段|BC|=4,BC中点为M,点A与B,C两点的距离之和为6,设|AM|=y,|AB|=x.(Ⅰ)求y=f(x)的函数表达式及函数的定义域;
(Ⅱ)设d=y+x-1,试求d的取值范围.
【答案】分析:(Ⅰ)分类讨论:A,B,C不共线时,根据三角形中线的性质可求得2(|BM|2+|AM|2)=|AB|2+|AC|2,进而利用两点间的距离公式代入等式中求得x和y的关系式;A,B,C三点共线时,|AB|+|AC|=6>|BC|推断出A在线段BC外侧,利用|6-x-x|=4求得x的值,代入2(|BM|2+|AM|2)=|AB|2+|AC|2也符合,从而可得函数f(x)的解析式,利用根号大于等于0的性质求得x的范围即函数的定义域.
(Ⅱ)确定函数解析式,利用导数的方法,即可求d的取值范围.
解答:解:(Ⅰ)当A、B、C三点不共线时,由三角形中线性质知2(|BM|2+|AM|2)=|AB|2+|AC|2,
代入得2(22+y2)=x2+(6-x)2,
又y≥0,得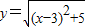 ;…(4分)
;…(4分)
当A,B,C三点共线时,由|AB|+|AC|=6>|BC|=4,可知A在线段BC外侧,
由|6-x-x|=4,可得x=1或x=5,因此,当x=1或x=5时,有|AB|+|AC|=6,
同时也满足:2(|BM|2+|AM|2)=|AB|2+|AC|2.
当A. B.C不共线时,||AB|-|AC||<|BC|=4,可知1<x<5,…(6分)
从而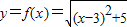 定义域为[1,5].…(7分)
定义域为[1,5].…(7分)
(Ⅱ)∵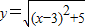 ,∴d=y+x-1=
,∴d=y+x-1=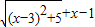 .
.
令t=x-3,由1≤x≤5知,t∈[-2,2],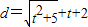 ,
,
两边对t求导得: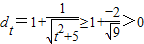 ,
,
∴d关于t在[-2,2]上单调递增.
∴当t=2时,dmin=3,此时x=1;当t=2时,dmax=7.此时x=5.
故d的取值范围为[3,7].…(15分)
点评:本题考查了两点间的距离公式的应用,考查函数思想的运用,考查导数知识的运用,考查了学生分析问题和解决问题的能力.
(Ⅱ)确定函数解析式,利用导数的方法,即可求d的取值范围.
解答:解:(Ⅰ)当A、B、C三点不共线时,由三角形中线性质知2(|BM|2+|AM|2)=|AB|2+|AC|2,
代入得2(22+y2)=x2+(6-x)2,
又y≥0,得
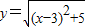 ;…(4分)
;…(4分)当A,B,C三点共线时,由|AB|+|AC|=6>|BC|=4,可知A在线段BC外侧,
由|6-x-x|=4,可得x=1或x=5,因此,当x=1或x=5时,有|AB|+|AC|=6,
同时也满足:2(|BM|2+|AM|2)=|AB|2+|AC|2.
当A. B.C不共线时,||AB|-|AC||<|BC|=4,可知1<x<5,…(6分)
从而
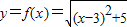 定义域为[1,5].…(7分)
定义域为[1,5].…(7分)(Ⅱ)∵
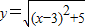 ,∴d=y+x-1=
,∴d=y+x-1=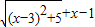 .
.令t=x-3,由1≤x≤5知,t∈[-2,2],
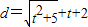 ,
,两边对t求导得:
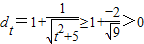 ,
,∴d关于t在[-2,2]上单调递增.
∴当t=2时,dmin=3,此时x=1;当t=2时,dmax=7.此时x=5.
故d的取值范围为[3,7].…(15分)
点评:本题考查了两点间的距离公式的应用,考查函数思想的运用,考查导数知识的运用,考查了学生分析问题和解决问题的能力.

练习册系列答案
相关题目