题目内容
如图(a),在直角梯形ABCD,∠B=90°,DC∥AB,动点P从B点出发,由B→C→D→A沿边运动,设点P运动的路程为x,△ABP的面积为y,如果关于y与x的函数图象如图(b),则△ABC的面积为( )
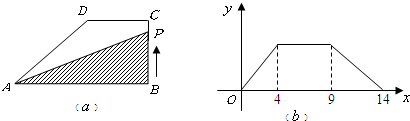

分析:根据图象关系建立y与x的函数关系式,根据关系式求三角形的面积.
解答: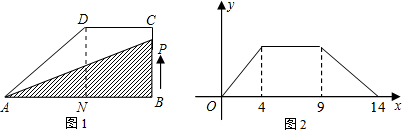 解:根据图2可知当点P在CD上运动时,△ABP的面积不变,与△ABC面积相等;且不变的面积是在x=4,x=9之间;
解:根据图2可知当点P在CD上运动时,△ABP的面积不变,与△ABC面积相等;且不变的面积是在x=4,x=9之间;
所以在直角梯形ABCD中BC=4,CD=5,AD=5.
过点D作DN⊥AB于点N,则有DN=BC=4,BN=CD=5,
在Rt△ADN中,AN=
=
=3
所以AB=BN+AN=5+3=8
所以△ABC的面积为
AB•BC=
×8×4=16.
故选B.
 解:根据图2可知当点P在CD上运动时,△ABP的面积不变,与△ABC面积相等;且不变的面积是在x=4,x=9之间;
解:根据图2可知当点P在CD上运动时,△ABP的面积不变,与△ABC面积相等;且不变的面积是在x=4,x=9之间;所以在直角梯形ABCD中BC=4,CD=5,AD=5.
过点D作DN⊥AB于点N,则有DN=BC=4,BN=CD=5,
在Rt△ADN中,AN=
| AD2-DN2 |
| 52-42 |
所以AB=BN+AN=5+3=8
所以△ABC的面积为
| 1 |
| 2 |
| 1 |
| 2 |
故选B.
点评:主要考查了函数图象的读图能力,能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,结合实际意义得到正确的结论.

练习册系列答案
相关题目


 (2013•宁德模拟)如图(1),在直角梯形 ABCD 中,AB∥CD,∠C=90°,CD=2AB=2,∠D=60°,E为DC中点,将四边形ABCE绕直线AE旋转90°得到四边形AB′C′E,
(2013•宁德模拟)如图(1),在直角梯形 ABCD 中,AB∥CD,∠C=90°,CD=2AB=2,∠D=60°,E为DC中点,将四边形ABCE绕直线AE旋转90°得到四边形AB′C′E, 如图(1),在直角梯形 ABCD 中,AB∥CD,∠C=90°,CD=2AB=2,∠D=60°,E为DC中点,将四边形ABCE绕直线AE旋转90°得到四边形AB′C′E,
如图(1),在直角梯形 ABCD 中,AB∥CD,∠C=90°,CD=2AB=2,∠D=60°,E为DC中点,将四边形ABCE绕直线AE旋转90°得到四边形AB′C′E,

