题目内容
设 是两个互相垂直的单位向量,已知向量
是两个互相垂直的单位向量,已知向量 且向量
且向量 ,
,(1)求f(k)的表达式.
(2)求f(k)的值域及夹角θ=60°时的k值.
(3)在(1)的条件下解关于k的不等式:
 .
.
【答案】分析:(1)由 ,
,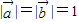 可求
可求 =2k,
=2k, =
= ,
, ,代入f(k)=cosθ=
,代入f(k)=cosθ= 可求
可求
(2)由1+2k2≥2k可得f(k)∈(0,1]结合θ=60°可知cosθ= ,可求k
,可求k
(3)由(1)可得f[f(k)]= =
=
 ?
? ,k>0,分类讨论:分a>0时,当a=0时,当a<0时,三种情况分别求解
,k>0,分类讨论:分a>0时,当a=0时,当a<0时,三种情况分别求解
解答:解:(1)∵ ∴
∴ ,
,
∵
∴ =
= =2k
=2k
∵ =
= ,同理可得
,同理可得
∴f(k)=cosθ= =
= (k>0)…(4分)
(k>0)…(4分)
(2)因为1+2k2≥2k当且仅当k=1时等号成立
所以f(k)∈(0,1],
当θ=60°时,cosθ=
∴ (8分)
(8分)
(3)由(1)可得f[f(k)]=f( )=
)= =
=

?4k3+4k<-3ak2+(4+a2)k
?k(4k2+3ak-a2)<0
? ,
,
∵k>0
当a>0时,解可得0<k<
当a=0时,解为k<0且k>0,此时k不存在
当a<0时,解为0<k<-a
综上所述:当a>0时,解集为{k|0<k< };
};
当a=0时,解集为∅
当a<0时,解集为{k|0<k<-a}(12分)
点评:本题主要考查了向量的数量积的应用,向量夹角公式的应用,及不等式的求解,属于综合试题
 ,
,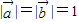 可求
可求 =2k,
=2k, =
= ,
, ,代入f(k)=cosθ=
,代入f(k)=cosθ= 可求
可求
(2)由1+2k2≥2k可得f(k)∈(0,1]结合θ=60°可知cosθ=
 ,可求k
,可求k(3)由(1)可得f[f(k)]=
 =
=
 ?
? ,k>0,分类讨论:分a>0时,当a=0时,当a<0时,三种情况分别求解
,k>0,分类讨论:分a>0时,当a=0时,当a<0时,三种情况分别求解解答:解:(1)∵
 ∴
∴ ,
,∵

∴
 =
= =2k
=2k∵
 =
= ,同理可得
,同理可得
∴f(k)=cosθ=
 =
= (k>0)…(4分)
(k>0)…(4分)(2)因为1+2k2≥2k当且仅当k=1时等号成立
所以f(k)∈(0,1],
当θ=60°时,cosθ=

∴
 (8分)
(8分)(3)由(1)可得f[f(k)]=f(
 )=
)= =
=

?4k3+4k<-3ak2+(4+a2)k
?k(4k2+3ak-a2)<0
?
 ,
,∵k>0
当a>0时,解可得0<k<

当a=0时,解为k<0且k>0,此时k不存在
当a<0时,解为0<k<-a
综上所述:当a>0时,解集为{k|0<k<
 };
};当a=0时,解集为∅
当a<0时,解集为{k|0<k<-a}(12分)
点评:本题主要考查了向量的数量积的应用,向量夹角公式的应用,及不等式的求解,属于综合试题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
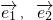 是两个互相垂直的单位向量,
是两个互相垂直的单位向量,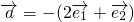 ,
,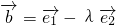 ,若
,若 ⊥
⊥ ,则λ的值为 ________.
,则λ的值为 ________. 是两个互相垂直的单位向量,
是两个互相垂直的单位向量, ,
, ,若
,若 ⊥
⊥ ,则λ的值为 .
,则λ的值为 .