题目内容
P,Q,M,N四点都在椭圆x2+| y2 |
| 2 |
| PF |
| FQ |
| MF |
| FN |
| PF |
| MF |
分析:由题设条件可知MN⊥PQ.设MN⊥y轴,则PQ⊥x轴,MN的方程为y=1,PQ的方程为x=0,由题设条件能够推出四边形PMQN的面积为
,|MN|•|PQ|=
×
×2
=2.当MN,PQ都不与坐标轴垂直时,根据题设条件能够推导出|MN|=
,|PQ|=
,所以S四边形PMQN=
|MN|•|PQ|=2(1-
)=2(1-
)≥
,由此入手结合题设条件能够导出(S四边形PMQN)max=2,(S四边形PMQN)min=
.
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
2
| ||
| k2+2 |
2
| ||
| 2k2+1 |
| 1 |
| 2 |
| k2 |
| 2k4+5k2+2 |
| 1 |
| 2(k2+1/k2)+5 |
| 16 |
| 9 |
| 16 |
| 9 |
解答: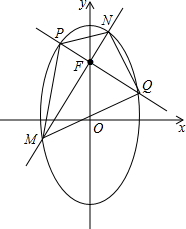 解:∵
解:∵
•
=0?
⊥
.即MN⊥PQ.
当MN或PQ中有一条直线垂直于x轴时,另一条直线必垂直于y轴.
不妨设MN⊥y轴,则PQ⊥x轴,
∵F(0,1)
∴MN的方程为:y=1,PQ的方程为:x=0
分别代入椭圆x2+
=1中得:|MN|=
,|PQ|=2
.
S四边形PMQN=
|MN|•|PQ|=
×
×2
=2
当MN,PQ都不与坐标轴垂直时,
设MN的方程为y=kx+1(k≠0),
代入椭圆x2+
=1中得:(k2+2)x2+2kx-1=0,
∴x1+x2=-
,x1•x2=-
∴|MN|=
=
=
同理可得:|PQ|=
,
S四边形PMQN=
|MN|•|PQ|=2×
=2(1-
)=2(1-
)≥
(当且仅当k2=
即k=±1时,取等号).
又S四边形PMQN=2(1-
)<2,∴此时
≤S四边形PMQN<2.
综上可知:(S四边形PMQN)max=2,(S四边形PMQN)min=
.
 解:∵
解:∵| PF |
| MF |
| PF |
| MF |
当MN或PQ中有一条直线垂直于x轴时,另一条直线必垂直于y轴.
不妨设MN⊥y轴,则PQ⊥x轴,
∵F(0,1)
∴MN的方程为:y=1,PQ的方程为:x=0
分别代入椭圆x2+
| y2 |
| 2 |
| 2 |
| 2 |
S四边形PMQN=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
当MN,PQ都不与坐标轴垂直时,
设MN的方程为y=kx+1(k≠0),
代入椭圆x2+
| y2 |
| 2 |
∴x1+x2=-
| 2k |
| k2+2 |
| 1 |
| k2+2 |
∴|MN|=
| (1+k2)[(x1+x2)2-4x1x2] |
(1+k2)[(
|
2
| ||
| k2+2 |
同理可得:|PQ|=
2
| ||
| 2k2+1 |
S四边形PMQN=
| 1 |
| 2 |
| 2k4+4k2+2 |
| 2k4+5k2+2 |
| k2 |
| 2k4+5k2+2 |
| 1 |
| 2(k2+1/k2)+5 |
| 16 |
| 9 |
(当且仅当k2=
| 1 |
| k2 |
又S四边形PMQN=2(1-
| k2 |
| 2k4+5k2+2 |
| 16 |
| 9 |
综上可知:(S四边形PMQN)max=2,(S四边形PMQN)min=
| 16 |
| 9 |
点评:本题综合考查椭圆的性质及其应用和直线与椭圆的位置关系,解题昌要认真审题,仔细解答,避免错误.

练习册系列答案
相关题目
 上,F为椭圆在y轴正半轴上的焦点.已知
上,F为椭圆在y轴正半轴上的焦点.已知 与
与 共
共 与
与 共线.求四边形PMQN的面积的最小值和最大值.
共线.求四边形PMQN的面积的最小值和最大值.