题目内容
若f(x)=2x2-kx-8在[2,6]上不具有单调性,则正实数k的取值范围是 ________.
[8,24]
分析:求出函数对称轴,由函数在[2,6]上不具有单调性,可知对称轴在此区间里,因而求出答案.
解答:函数对称轴为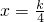 ,
,
由f(x)=2x2-kx-8在[2,6]上不具有单调性,
因而可知对称轴在此区间里,即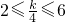 ,
,
解得8≤k≤24,
故答案为[8,24].
点评:此题主要考查函数单调性和对称轴的求解.
分析:求出函数对称轴,由函数在[2,6]上不具有单调性,可知对称轴在此区间里,因而求出答案.
解答:函数对称轴为
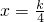 ,
,由f(x)=2x2-kx-8在[2,6]上不具有单调性,
因而可知对称轴在此区间里,即
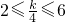 ,
,解得8≤k≤24,
故答案为[8,24].
点评:此题主要考查函数单调性和对称轴的求解.

练习册系列答案
相关题目
若f(x)=2x2-1(-
<x<
),f(a)=7,则a的值是( )
| 3 |
| 5 |
| A、1 | B、-1 | C、2 | D、±2 |