题目内容
已知向量m=(cosx,sinx),n=(cosx,cosx)(x∈R),设函数f(x)=m·n
(1)求 f(x)的解析式,并求最小正周期.
(2)若函数 g(x)的图像是由函数 f(x)的图像向右平移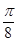 个单位得到的,求g(x)的最大值及使g(x)取得最大值时x的值.
个单位得到的,求g(x)的最大值及使g(x)取得最大值时x的值.
(1)求 f(x)的解析式,并求最小正周期.
(2)若函数 g(x)的图像是由函数 f(x)的图像向右平移
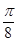 个单位得到的,求g(x)的最大值及使g(x)取得最大值时x的值.
个单位得到的,求g(x)的最大值及使g(x)取得最大值时x的值. (1) ,最小正周期为
,最小正周期为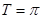 ;
;
(2)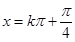
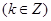 时
时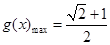
 ,最小正周期为
,最小正周期为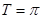 ;
;(2)
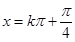
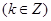 时
时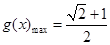
本试题主要是考查了三角函数的性质的运用。
(1)因为向量m=(cosx,sinx),n=(cosx,cosx)(x∈R),则函数f(x)=m·n
可以运用向量的数量积表示为单一三角函数,并求解周期。
(2)当将函数 g(x)的图像是由函数 f(x)的图像向右平移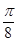 个单位得到的,
个单位得到的,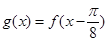 利用三角函数的性质得到最值。
利用三角函数的性质得到最值。
解:(1)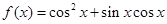
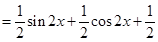
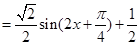 (x∈R),∴f(x)的最小正周期为
(x∈R),∴f(x)的最小正周期为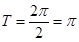
(2)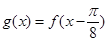
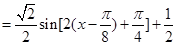
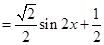
∴当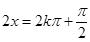 ,即
,即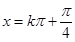
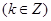 时
时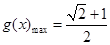
(1)因为向量m=(cosx,sinx),n=(cosx,cosx)(x∈R),则函数f(x)=m·n
可以运用向量的数量积表示为单一三角函数,并求解周期。
(2)当将函数 g(x)的图像是由函数 f(x)的图像向右平移
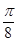 个单位得到的,
个单位得到的,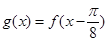 利用三角函数的性质得到最值。
利用三角函数的性质得到最值。解:(1)
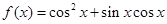
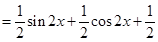
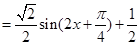 (x∈R),∴f(x)的最小正周期为
(x∈R),∴f(x)的最小正周期为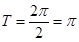
(2)
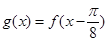
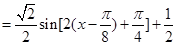
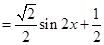
∴当
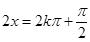 ,即
,即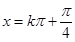
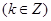 时
时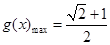

练习册系列答案
相关题目
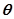 是第一象限角,试确定
是第一象限角,试确定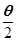 的象限.
的象限.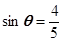 ,求
,求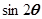 的值.
的值. 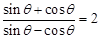 ,求
,求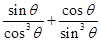 的值
的值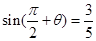 ,则
,则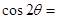 .
.
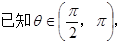 sin
sin ,则tan
,则tan =_____________。
=_____________。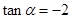 ,则
,则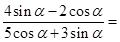 _______________.
_______________.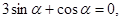 则
则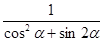 的值为
的值为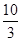
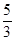
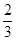
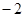
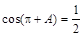 ,则
,则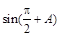 的值是( )
的值是( )