题目内容
(在给出的二个题中,任选一题作答.若多选做,则按所做的第一题给分)
(1)(坐标系与参数方程)在极坐标系中,曲线ρcos2θ=2sinθ的焦点的极坐标为
(2)(不等式选讲)若不等式
≥x(a>0)的解集为{x|m≤x≤n},且|m-n|=2a,则a的取值集合为
(1)(坐标系与参数方程)在极坐标系中,曲线ρcos2θ=2sinθ的焦点的极坐标为
(
,
)
| 1 |
| 2 |
| π |
| 2 |
(
,
)
.| 1 |
| 2 |
| π |
| 2 |
(2)(不等式选讲)若不等式
| x+a |
{2}
{2}
.分析:(1)若点P在直角坐标系中的坐标为(x,y),在极坐标系中的坐标为(ρ,θ),则有关系式:
.根据此公式将曲线转化成x2=2y,得到曲线是开口向上的抛物线,以F(0,
)为焦点,再将点F化成极坐标即可;
(2)根据题意,不等式的解集应该是曲线y=
位于直线y=x上方的部分为符合题意的图象,观察其横坐标,可得x=n是方程
=x的一个解,且|m-n|=m+a=2a,建立方程组,解之可得a的取值集合.
|
| 1 |
| 2 |
(2)根据题意,不等式的解集应该是曲线y=
| x+a |
| x+a |
解答:解:(1)由ρcos2θ=2sinθ得ρ2cos2θ=2ρsinθ
∵x=ρcosθ,y=ρsinθ
∴曲线的直角坐标方程为:x2=2y,是以F(0,
)为焦点,开口向上的抛物线,
再将F化成极坐标形式为:(
,
)
(2)根据不等式
≥x作出如右图的示意图,
曲线y=
位于直线y=x上方的部分为符合题意的图象,观察其横坐标
可得区间[m,n]即[-a,n],说明(n,0)在曲线y=
-x上
即:
解之得:n=a=2
故答案为:(
,
),{2}

∵x=ρcosθ,y=ρsinθ
∴曲线的直角坐标方程为:x2=2y,是以F(0,
| 1 |
| 2 |
再将F化成极坐标形式为:(
| 1 |
| 2 |
| π |
| 2 |
(2)根据不等式
| x+a |
曲线y=
| x+a |
可得区间[m,n]即[-a,n],说明(n,0)在曲线y=
| x+a |
即:
|
解之得:n=a=2
故答案为:(
| 1 |
| 2 |
| π |
| 2 |
点评:本题第一小问考查了简单曲线的极坐标方程,以及极坐标与直角坐标的互化,第二小问考查了不等式的解集求法和不等式的基本性质,都属于中档题.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
 与圆
与圆 的位置关系是 。
的位置关系是 。 ,不等式
,不等式 恒成立,则实数
恒成立,则实数 的取值范围是 。
的取值范围是 。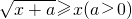 的解集为{x|m≤x≤n},且|m-n|=2a,则a的取值集合为________.
的解集为{x|m≤x≤n},且|m-n|=2a,则a的取值集合为________. 的解集为{x|m≤x≤n},且|m-n|=2a,则a的取值集合为______.
的解集为{x|m≤x≤n},且|m-n|=2a,则a的取值集合为______.