题目内容
已知向量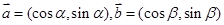 ,并且满足关系:
,并且满足关系: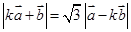
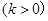 ,则
,则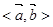 的最大值为 ( )
的最大值为 ( )
A.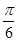 | B.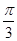 | C.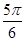 | D.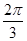 |
B
解析试题分析:因为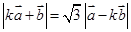 ,所以
,所以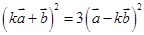 ,
,
即 (*)因为
(*)因为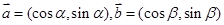 ,所以
,所以 ,
, ,代入(*)式,
,代入(*)式,
得 整理得
整理得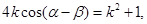 因为
因为 ,所以
,所以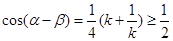 ,所以
,所以 所以
所以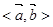 的最大值为
的最大值为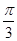 .
.
考点:本小题考查向量的基本运算及利用基本不等求最值.
点评:高考中,主要考查利用数量积解决垂直、长度、夹角等问题,有时还与三角函数、解析几何结合在一起出题.对于这类问题,学生要熟练应用公式,准确计算.

练习册系列答案
相关题目
在 中,
中, ,
, ,
, 分别是角
分别是角 ,
, ,
, 的对边,
的对边, ,
, ,且
,且 ,则
,则 的
的 边上的高等于( )
边上的高等于( )
A. | B. | C. | D. |
若 ,
, ,则sin
,则sin =( )
=( )
A. | B. | C. | D. |
设 是方程
是方程 的两个根,则
的两个根,则 的值为
的值为
| A.-3 | B.-1 | C.1 | D.3 |
为了得到函数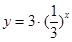 的图象,可以把函数
的图象,可以把函数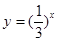 的图象
的图象
| A.向左平移3个单位长度 | B.向右平移3个单位长度 |
| C.向左平移1个单位长度 | D.向右平移1个单位长度 |
若 ,则
,则 的值为( )
的值为( )
A. | B. | C. | D. |
已知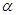 是第四象限角,且
是第四象限角,且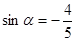 ,则
,则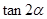 的值为( )
的值为( )
A.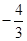 | B.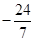 | C. | D.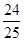 |
 ( )
( )
A. | B. | C. | D. |
若 的内角
的内角 满足
满足 ,则
,则 ( )
( )
A. | B. | C. | D. |