题目内容
已知某函数的导数为y′=
,则这个函数可能是( )
| 1 |
| 2(x-1) |
A、y=ln
| ||||
B、y=ln
| ||||
| C、y=ln(1-x) | ||||
D、y=ln
|
分析:利用复合函数的导数法则依次对选项的函数求导数,结合题意,可得答案.
解答:解:对选项求导.
A、(ln
)′=
(
)′=
•
(1-x)-
•(-1)=
,符合;
对于B,∵y=-ln
,∴y′=-
,不符合;
对于C,y′=
•(1-x)′=-
,不符合;
对于D,∵y=-ln(x-1)∴y′=-
,不符合;
故选A
A、(ln
| 1-x |
| 1 | ||
|
| 1-x |
| 1 | ||
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2(x-1) |
对于B,∵y=-ln
| 1-x |
| 1 |
| 2(x-1) |
对于C,y′=
| 1 |
| 1-x |
| 1 |
| 1-x |
对于D,∵y=-ln(x-1)∴y′=-
| 1 |
| x-1 |
故选A
点评:本题考查复合函数的导数法则:内函数的导数乘以外函数的导数.

练习册系列答案
相关题目
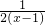 ,则这个函数可能是
,则这个函数可能是
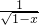

 ,则这个函数可能是( )
,则这个函数可能是( )

