题目内容
(满分12分)设函数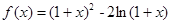 。
。
(Ⅰ)若在定义域内存在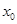 ,而使得不等式
,而使得不等式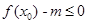 能成立,求实数
能成立,求实数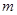 的最小值;
的最小值;
(Ⅱ)若函数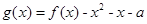 在区间
在区间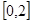 上恰有两个不同的零点,求实数
上恰有两个不同的零点,求实数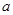 的取值范围。
的取值范围。
【答案】
(Ⅰ)实数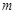 的最小值为
的最小值为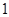 。(Ⅱ)
。(Ⅱ)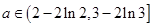 。
。
【解析】
试题分析:(Ⅰ)要使得不等式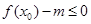 能成立,只需
能成立,只需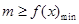 。
。
求导得: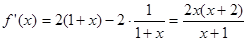 ,
………3分
,
………3分
∵函数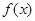 的定义域为
的定义域为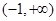 ,
,
当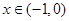 时,
时,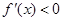 ,∴函数
,∴函数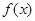 在区间
在区间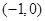 上是减函数;
上是减函数;
当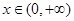 时,
时,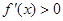 ,∴函数
,∴函数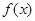 在区间(0,+∞)上是增函数。
在区间(0,+∞)上是增函数。
∴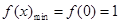 , ∴
, ∴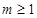 。故实数
。故实数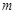 的最小值为
的最小值为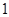 。
………6分
。
………6分
(Ⅱ)由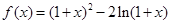 得:
得:
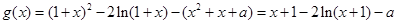
由题设可得:方程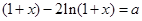 在区间
在区间 上恰有两个相异实根………8分
上恰有两个相异实根………8分
设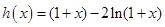 。∵
。∵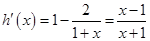 ,列表如下:
,列表如下:
|
|
|
|
|
|
|
|
|
|
- |
0 |
+ |
|
|
|
|
减函数 |
|
增函数 |
|
∵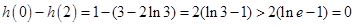 ,
,
∴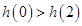 。
。
从而有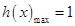 ,
,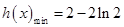 ………10分
………10分
画出函数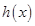 在区间
在区间 上的草图
上的草图
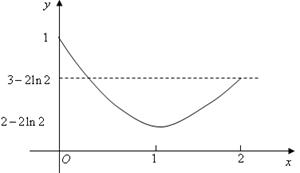
易知要使方程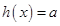 在区间
在区间 上恰有两个相异实根,
上恰有两个相异实根,
只需: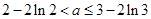 ,即:
,即: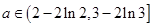 。
………12分
。
………12分
考点:本题主要考查导数的应用,研究函数单调性、确定函数最值、研究函数图象。
点评:利用导数研究函数单调性、确定函数最值、研究函数图象,是导数的基本应用。本题将“恒成立”问题转化成求函数最值问题,将函数零点问题,转化成研究函数单调性、求最值问题,凸显转化与化归数学的重要性。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
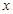
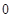
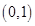
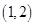
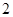
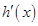
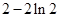
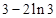
 ,
, 的图象的一条对称轴是直线
的图象的一条对称轴是直线 .
.
 ;
; ]上的图象.
]上的图象.
 的值域;
的值域; BC的内角A.B.C的对边长分别为
BC的内角A.B.C的对边长分别为 的值。
的值。 (其中
(其中 ),且
),且 的图象在
的图象在 轴右侧的第一个最高点的横坐标为
轴右侧的第一个最高点的横坐标为 。
。 的值。
的值。 上的最小值为
上的最小值为 ,求
,求 的值。
的值。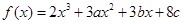 在
在 及
及 时取得极值;
时取得极值; 与b的值;
与b的值; ,都有
,都有 成立,求c的取值范围。
成立,求c的取值范围。