题目内容
已知一个棱长为2的正方体,被一个平面截后所得几何体的三视图如图所示,则该几何体的体积是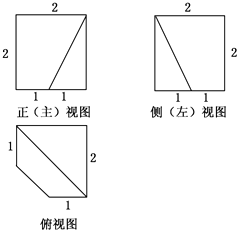
分析:由三视图可以得出,此几何体可以看作是一个边长为2的正方体被截去了一个棱台而得到,此棱台的高为2,一底为直角边长为2的等腰直角三角形,一底为直角边长为1的等腰直角三角形,几何体的体积易求
解答:解:由三视图知,此几何体可以看作是一个边长为2的正方体被截去了一个棱台而得到,此棱台的高为2,一底为直角边长为2的等腰直角三角形,一底为直角边长为1的等腰直角三角形,
棱台的两底面的面积分别为
×2×2=2,
×1×1=
该几何体的体积是2×2×2-
×2×(
+2+
)=8-
=
故答案为:
.
棱台的两底面的面积分别为
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
该几何体的体积是2×2×2-
| 1 |
| 3 |
| 1 |
| 2 |
2×
|
| 7 |
| 3 |
| 17 |
| 3 |
故答案为:
| 17 |
| 3 |
点评:本题考查由三视图求面积、体积,解答本题,关键是由三视图得出几何体的几何特征,以及几何体的长宽高等几何数据,本题中由于几何体形状特殊,采取了补法求体积,割补法求体积,是几何中转化求体积的常用技巧,适合不规则几何体的体积求法

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知球O在一个棱长为2
的正四面体内,如果球O是该正四面体的最大球,那么球O的表面积等于( )
| 3 |
A、4
| ||||
B、
| ||||
| C、2π | ||||
D、
|
 (2011•佛山二模)如图,已知几何体的下部是一个底面是边长为2的正六边形、侧面全为正方形的棱柱,上部是一个侧面全为等腰三角形的棱锥,其侧棱长都为
(2011•佛山二模)如图,已知几何体的下部是一个底面是边长为2的正六边形、侧面全为正方形的棱柱,上部是一个侧面全为等腰三角形的棱锥,其侧棱长都为
 .
.