题目内容
已知点P是棱长为
的正八面体的一个对角面上的一个动点,若P到不在该对角面上的一个顶点的距离是它到在该对角面上的某个顶点的距离的
倍,则动点P的轨迹是( )的部分.
| 2 |
| 2 |
| A、圆 | B、抛物线 | C、双曲线 | D、椭圆 |
分析:由阿波罗尼圆问题,我们可以类比推断出在空间中到两个定点的距离之比为宣传的动点轨迹为一个球,结合P点是正八面体的一个对角面上的一个动点,故我们可将问题转化为一个平面与球的截面形状判定问题,结合球的几何特征即可得到答案.
解答:解:设不在该对角面上的一个顶点为A,
在该对角面上的某个顶点为B
若P点到A的距离为P点到B点距离的
倍,
则P点的轨迹为一个球
又由题目中P点是正八面体的一个对角面上的一个动点,
该平面截上述球所得的轨迹为一个圆
故选A
在该对角面上的某个顶点为B
若P点到A的距离为P点到B点距离的
| 2 |
则P点的轨迹为一个球
又由题目中P点是正八面体的一个对角面上的一个动点,
该平面截上述球所得的轨迹为一个圆
故选A
点评:本题考查的是到两个定点的距离的比为定值的动点轨迹,即是阿波罗尼圆问题.但在空间中,到两个定点的距离之比为宣传的动点轨迹为一个球,本题是一个平面截球的截面形状判定问题.

练习册系列答案
相关题目
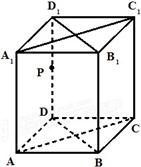 已知ABCD-A1B1C1D1是底面为菱形的直四棱柱,P是棱DD1的中点,∠BAD=60°,底面边长为2,若PB与平面ADD1A1成45°角,求点A1到平面ACP的距离.
已知ABCD-A1B1C1D1是底面为菱形的直四棱柱,P是棱DD1的中点,∠BAD=60°,底面边长为2,若PB与平面ADD1A1成45°角,求点A1到平面ACP的距离.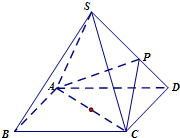 已知四棱椎S-ABCD中,底面是边长为2的正方形,每条侧棱长都是
已知四棱椎S-ABCD中,底面是边长为2的正方形,每条侧棱长都是