题目内容
已知曲线x2+2y2+4x+4y+4=0按向量a=(2,1)平移后得到曲线C.(1)求曲线C的方程;
(2)过点D(0,2)的直线与曲线C相交于不同的两点M、N,且M在D、N之间,设
| DM |
| MN |
分析:(1)原曲线即为(x+2)2+2(y+1)2=2,按向量a=(2,1)平移即是把函数向右平移2个单位,向上平移1个单位后得到曲线C.
(2)设M(x1,y1),N(x2,y2),由
=λ
,可得
由点M、N在椭圆x2+2y2=2上,代入方程整理可得即y2=
.结合椭圆的性质可知-1≤y2≤1,代入可求λ的取值范围.
(2)设M(x1,y1),N(x2,y2),由
| DM |
| MN |
|
| 2λ-3 |
| 4λ |
解答:解:(1)原曲线即为(x+2)2+2(y+1)2=2,则平移后的曲线C为x2+2y2=2,
即
+y2=1.
(2)设M(x1,y1),N(x2,y2),则
由于点M、N在椭圆x2+2y2=2上,则
即
消去x22得,2λ2+8λy2+8=2λ2+4λ+2,
即y2=
.
∵-1≤y2≤1,
∴-1≤
≤1.
又∵λ>0,故解得λ≥
.
故λ的取值范围为[
,+∞).
思考讨论本题:若设出直线l的方程y=kx+2,然后与x2+2y2=2联立,利用韦达定理能求解吗?(不要忘记讨论斜率不存在的情况)读者可尝试一下.
即
| x2 |
| 2 |
(2)设M(x1,y1),N(x2,y2),则
|
|
即
|
消去x22得,2λ2+8λy2+8=2λ2+4λ+2,
即y2=
| 2λ-3 |
| 4λ |
∵-1≤y2≤1,
∴-1≤
| 2λ-3 |
| 4λ |
又∵λ>0,故解得λ≥
| 1 |
| 2 |
故λ的取值范围为[
| 1 |
| 2 |
思考讨论本题:若设出直线l的方程y=kx+2,然后与x2+2y2=2联立,利用韦达定理能求解吗?(不要忘记讨论斜率不存在的情况)读者可尝试一下.
点评:本题主要考查了曲线的平移,向量共线的坐标表示,直线与椭圆的相交关系的综合应用,试题的思路比较清晰,但需要考生具备一定的运算能力及逻辑推理能力.

练习册系列答案
相关题目
 =λ
=λ ,求实数λ的取值范围.
,求实数λ的取值范围.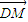 =λ
=λ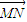 ,求实数λ的取值范围.
,求实数λ的取值范围.