题目内容
在函数y=|tanx|,y=|sin(x+
)|,y=|sin2x|,y=sin(2x-
)四个函数中,既是以π为周期的偶函数,又是区间(0,
)上的增函数个数是( )
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| A、1 | B、2 | C、3 | D、4 |
分析:分别画出函数y=|tanx|,y=|sin(x+
)|,y=|sin2x|的图象,即可判断出是否满足条件;再由诱导公式对y=sin(2x-
)进行化简,根据余弦函数的性质可得到答案.
| π |
| 2 |
| π |
| 2 |
解答:解:y=|tanx|,的图象如下
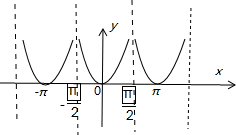
满足条件;
y=|sin(x+
)|=|cosx|的图象为
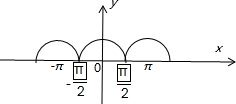
不满足条件;
y=|sin2x|的图象如图
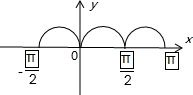
不满足条件;
y=sin(2x-
)=-cos2x,T=
=π,以π为周期的偶函数,
再由余弦函数的单调性知在(0,
)上是增函数;
故选B.

满足条件;
y=|sin(x+
| π |
| 2 |

不满足条件;
y=|sin2x|的图象如图

不满足条件;
y=sin(2x-
| π |
| 2 |
| 2π |
| 2 |
再由余弦函数的单调性知在(0,
| π |
| 2 |
故选B.
点评:本题主要考查带绝对值的三角函数的图象和性质的应用.考查三角函数的对称性和单调性,三角函数的图象是高考的重点,一定要会画图.

练习册系列答案
相关题目
 )|,y=|sin2x|,y=sin(2x-
)|,y=|sin2x|,y=sin(2x- )|,y=|sin2x|,y=sin(2x-
)|,y=|sin2x|,y=sin(2x-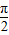 )四个函数中,既是以π为周期的偶函数,又是区间(0,
)四个函数中,既是以π为周期的偶函数,又是区间(0, )上的增函数个数是( )
)上的增函数个数是( )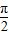 )|,y=|sin2x|,y=sin(2x-
)|,y=|sin2x|,y=sin(2x-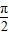 )四个函数中,既是以π为周期的偶函数,又是区间(0,
)四个函数中,既是以π为周期的偶函数,又是区间(0,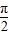 )上的增函数个数是( )
)上的增函数个数是( )